প্রিয় পাঠকগণ, আমি আজ আপনাদের সাথে শেয়ার করব হয়ত সবচেয়ে সহজ কিন্তু গুরুত্বপূর্ণ ত্রিভুজ সম্পর্কে - সমকোণী ত্রিভুজ।
ত্রিভুজের তিনটি কোণ থাকে যার মধ্যে যদি কোন একটি কোণ ৯০ ডিগ্রি হয়, তাহলে সেটিকে সমকোণী ত্রিভুজ বলা হয়।
গণিতের বিভিন্ন অংশ শেখার সময় আমরা অনেক সময়ই সমকোণী ত্রিভুজের সাথে পরিচিত হই। এটি খুব সহজ হলেও অনেক গুরুত্বপূর্ণ ত্রিভুজের মধ্যে অন্যতম। তাই আজ আমরা সমকোণী ত্রিভুজের বৈশিষ্ট্য, গুণাবলী এবং কিছু উদাহরণের মাধ্যমে এটির গুরুত্ব সম্পর্কে আলোচনা করব।
আশা করি এই পোস্ট থেকে আপনারা সমকোণী ত্রিভুজ সম্পর্কে কিছু নতুন জানতে পারবেন। তা হলে আসুন শুরু করা যাক আমাদের আলোচনা।
সমকোণী ত্রিভুজে থাকে মাত্র একটি সমকোণ। সেই সমকোণ ছাড়া অবশিষ্ট দুইটি কোণ হচ্ছে সূক্ষ্মকোণ।
সমকোণী ত্রিভুজে, যেহেতু একটি কোণ সমকোণ বা ৯০ ডিগ্রি, সেহেতু অবশিষ্ট দুইটি সূক্ষ্মকোণের মোট পরিমাণ অবশ্যই ৯০ ডিগ্রি হবে।
কারণ ত্রিভুজের কোণগুলোর মোট পরিমাণ ১৮০ ডিগ্রি। সুতরাং, যদি একটি কোণ ৯০ ডিগ্রি হয়, তাহলে বাকি দুইটি কোণের মোট পরিমাণ ৯০ ডিগ্রি হয়েই থাকবে।
এছাড়াও, কোনো ত্রিভুজে দুইটির বেশি সমকোণ থাকা যায় না, কারণ তখন মোট কোণ ১৮০ ডিগ্রির বেশি হয়ে যাবে।
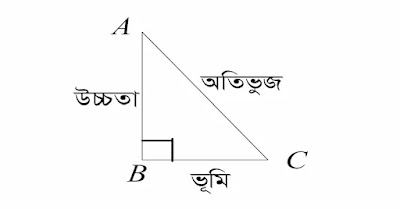
চিত্রে, ABC ত্রিভুজটি একটি সমকোণী ত্রিভুজ, যার ∆ABC সমকোণ। কিন্তু এর অন্য দুইটি কোণের প্রত্যেকটি সূক্ষ্মকোণ হবে। অর্থাৎ BAC ও BCA উভয়ই সুক্ষ্মকোণ।
সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ ( Hypotenuse) বলে এবং সমকোণ সংলগ্ন বাহুর একটিকে ভূমি (Base) ও অপরটিকে উন্নতি বা উচ্চতা ( Altitude) ধরা হয়।
চিত্রে, ABC সমকোণী ত্রিভুজের AC বাহু অতিভুজ এবং BC বাহু ভূমি ও AB বাহু উচ্চতা।
এর বৈশিষ্ট্যগুলি:
এর উপর ভিত্তি করেই এটিকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলা হয়।
এর বৈশিষ্ট্যগুলি:
সুতরাং, যেহেতু এতে দুইটি পাশের দৈর্ঘ্য সমান নয় এবং একটি কোণ সোজা কোণ, সেহেতু এটিকে সমকোণী বিষমবাহু ত্রিভুজ বলা হয়।
1. একটি রেখারেখক নিন এবং এর মধ্যে একটি বিন্দু নির্বাচন করুন। এটি হবে আপনার ত্রিভুজের একটি কোণাকার বিন্দু।
2. প্রথম কোণাকার বিন্দু থেকে একটি সোজা রেখা অঙ্কন করুন। এটি হবে আপনার ত্রিভুজের একটি পাশ।
3. প্রথম বিন্দু থেকে আরেকটি রেখা অঙ্কন করুন যেটি প্রথম রেখার সাথে 90 ডিগ্রি কোণ বন্ধ করবে। এটি হবে আপনার ত্রিভুজের দ্বিতীয় পাশ।
4. দুই পাশ থেকে রেখাগুলি বাড়িয়ে তৃতীয় বিন্দুতে সংযুক্ত করুন। এটি হবে আপনার ত্রিভুজের তৃতীয় কোণাকার বিন্দু।
5. তিনটি কোণাকার বিন্দু সংযুক্ত করে ত্রিভুজটি পূর্ণ করুন।
এভাবে একটি সমকোণী ত্রিভুজের অঙ্কন সম্পন্ন হয়। পাশগুলির দৈর্ঘ্য পরিবর্তন করে সমদ্বিবাহু বা বিষমবাহু ত্রিভুজ অঙ্কন করা যায়।
সমকোণী ত্রিভুজের এই সূত্র সমূহ অনেক গুরুত্বপূর্ণ। বিভিন্ন হিসাব-নিকাশ, ক্ষেত্রফল ইত্যাদি বের করার ক্ষেত্রে এগুলো খুবই কাজে লাগে।
সমকোণী ত্রিভুজের ক্ষেত্রফল হলো সেই ত্রিভুজের আন্তরিক এলাকার পরিমাণ।
অর্থাৎ,
সমকোণী ত্রিভুজের ক্ষেত্রফল = ½ × সমকোণ সংলগ্ন বাহুদ্বয়ের গুণফল
একটি উদাহরণ দেখা যাক:
ধরুন একটি সমকোণী ত্রিভুজের ভূমি হল 5 সেন্টিমিটার এবং উচ্চতা 7 সেন্টিমিটার, তাহলে সমকোণী ত্রিভুজের ক্ষেত্রফল কত?
তাহলে,
সুতরাং, ক্ষেত্রফল = ½ x 5 x 7 = 17.5 বর্গ সেন্টিমিটার।
আবার এভাবেও, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র হল:
S = (½) x b x c x sinA
এখানে,
সূত্রে, দুইটি পাশের দৈর্ঘ্য b ও c এর গুণফলের অর্ধেককে sin 90° দিয়ে গুণ করা হয়। যেহেতু সমকোণের sin মান 1, সুতরাং সূত্রে sinA হিসাব করা হয়না।
এই সূত্রটি ব্যবহার করে সহজেই সমকোণী ত্রিভুজের ক্ষেত্রফল বের করা যায়।
যেমন, যদি একটি সমকোণী ত্রিভুজের দুই পাশের দৈর্ঘ্য যদি 5 সেন্টিমিটার এবং 7 সেন্টিমিটার হয়, তাহলে ক্ষেত্রফল হবেঃ
S = (1/2) x 5 x 7 = 17.5 বর্গ সেন্টিমিটার
সুতরাং, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র খুবই গুরুত্বপূর্ণ এবং ব্যবহারযোগ্য।
সমকোণী ত্রিভুজে থাকে তিনটি বাহু এবং একটি ৯০ ডিগ্রির কোণ। এই তিনটি বাহুর দৈর্ঘ্যগুলোকে যোগ করলে পাওয়া যায় সমকোণী ত্রিভুজের মোট পরিসীমা।
অর্থাৎ, সমকোণী ত্রিভুজের পরিসীমা = অতিভুজ + ভূমি + উচ্চতা।
সংক্ষেপে, সমকোণী ত্রিভুজের পরিসীমা হলো সেই ত্রিভুজের তিনটি বাহুর মোট দৈর্ঘ্য।
সমকোণী ত্রিভুজের পরিসীমা = অতিভুজ + ভূমি + উচ্চতা।
অর্থাৎ, যদি সমকোণ সংলগ্ন ভূমি দৈর্ঘ্য যদি a এবং উচ্চতা b একক এবং অতিভুজের দৈর্ঘ্য যদি c একক হয়, তাহলে পরিসীমা = a + b + c
উদাহরণস্বরূপ, যদি একটি সমকোণী ত্রিভুজের দুই বাহুর দৈর্ঘ্য যদি 4 সেন্টিমিটার এবং 6 সেন্টিমিটার এবং অতিভুজের দৈর্ঘ্য 8 সেন্টিমিটার হয়, তাহলে পরিসীমা =
a + b + c
= 4 + 6 + 8
= 18 সেন্টিমিটার
a² = b² + c² - 2bcCosA
যেখানে,
এই সূত্রের ব্যাখ্যা:
সমকোণী ত্রিভুজের দুই পাশ ও একটি অতিভুজ আছে। পাশদ্বয়ের দৈর্ঘ্য যদি b ও c হয়, এবং পাশদ্বয়ের মধ্যবর্তী কোণ A হয়, তাহলে অতিভুজের দৈর্ঘ্য a হিসেবে পাওয়া যায় এই সূত্র দ্বারা।
উদাহরণ:
যদি একটি সমকোণী ত্রিভুজে,
b = 3 ইউনিট
c = 4 ইউনিট
এবং A = 60 ডিগ্রি
তাহলে,
সমকোণী ত্রিভুজের অতিভুজের সূত্রে স্থাপন করলে,
a² = 3² + 4² - 2 x 3 x 4 x cos90°
a² = 9 + 16 - 24
a² = 1
∴ a = 1 ইউনিট
অর্থাৎ উপরোক্ত তথ্য ব্যবহার করে অতিভুজের দৈর্ঘ্য 1 ইউনিট পাওয়া গেল।
সুতরাং, সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য নির্ণয় করতে এই সূত্রটি ব্যবহার করা হয়।
যদি সমকোণী ত্রিভুজে,
তাহলে,
a² + b² = c²
অর্থাৎ প্রথম ও দ্বিতীয় বাহুর বর্গের সমষ্টি = তৃতীয় বাহুর বর্গ।
এই সূত্র ব্যবহার করে সমকোণী ত্রিভুজের যে কোন দুটি বাহুর দৈর্ঘ্য জেনে তৃতীয় বাহুর দৈর্ঘ্য বের করা যায়।
উদাহরণ:
যদি a = 3 ইউনিট এবং b = 4 ইউনিট
তাহলে,
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
অতএব, c = 5 ইউনিট
সুতরাং, তৃতীয় বাহুর দৈর্ঘ্য = 5 ইউনিট।
ত্রিভুজের তিনটি কোণ থাকে যার মধ্যে যদি কোন একটি কোণ ৯০ ডিগ্রি হয়, তাহলে সেটিকে সমকোণী ত্রিভুজ বলা হয়।
গণিতের বিভিন্ন অংশ শেখার সময় আমরা অনেক সময়ই সমকোণী ত্রিভুজের সাথে পরিচিত হই। এটি খুব সহজ হলেও অনেক গুরুত্বপূর্ণ ত্রিভুজের মধ্যে অন্যতম। তাই আজ আমরা সমকোণী ত্রিভুজের বৈশিষ্ট্য, গুণাবলী এবং কিছু উদাহরণের মাধ্যমে এটির গুরুত্ব সম্পর্কে আলোচনা করব।
আশা করি এই পোস্ট থেকে আপনারা সমকোণী ত্রিভুজ সম্পর্কে কিছু নতুন জানতে পারবেন। তা হলে আসুন শুরু করা যাক আমাদের আলোচনা।
সমকোণ ত্রিভুজ কাকে বলে :-
কোনো ত্রিভুজের একটি কোণ সমকোণ হলে, ত্রিভুজটিকে সমকোণী ত্রিভুজ বলা হয়।সমকোণী ত্রিভুজে থাকে মাত্র একটি সমকোণ। সেই সমকোণ ছাড়া অবশিষ্ট দুইটি কোণ হচ্ছে সূক্ষ্মকোণ।
সমকোণী ত্রিভুজে, যেহেতু একটি কোণ সমকোণ বা ৯০ ডিগ্রি, সেহেতু অবশিষ্ট দুইটি সূক্ষ্মকোণের মোট পরিমাণ অবশ্যই ৯০ ডিগ্রি হবে।
কারণ ত্রিভুজের কোণগুলোর মোট পরিমাণ ১৮০ ডিগ্রি। সুতরাং, যদি একটি কোণ ৯০ ডিগ্রি হয়, তাহলে বাকি দুইটি কোণের মোট পরিমাণ ৯০ ডিগ্রি হয়েই থাকবে।
এছাড়াও, কোনো ত্রিভুজে দুইটির বেশি সমকোণ থাকা যায় না, কারণ তখন মোট কোণ ১৮০ ডিগ্রির বেশি হয়ে যাবে।
চিত্রে, ABC ত্রিভুজটি একটি সমকোণী ত্রিভুজ, যার ∆ABC সমকোণ। কিন্তু এর অন্য দুইটি কোণের প্রত্যেকটি সূক্ষ্মকোণ হবে। অর্থাৎ BAC ও BCA উভয়ই সুক্ষ্মকোণ।
সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ ( Hypotenuse) বলে এবং সমকোণ সংলগ্ন বাহুর একটিকে ভূমি (Base) ও অপরটিকে উন্নতি বা উচ্চতা ( Altitude) ধরা হয়।
চিত্রে, ABC সমকোণী ত্রিভুজের AC বাহু অতিভুজ এবং BC বাহু ভূমি ও AB বাহু উচ্চতা।
সমকোণী ত্রিভুজ কত প্রকার ও কি কি:-
সমকোণী ত্রিভুজ দুই প্রকার। যথা- সমকোণী সমদ্বিবাহু ত্রিভুজ এবং
- সমকোণী বিষমবাহু ত্রিভুজ
সমকোণী সমদ্বিবাহু ত্রিভুজ কাকে বলে :-
সমকোণী সমদ্বিবাহু ত্রিভুজ সেই ত্রিভুজ যেখানে দুইটি পাশ সমান দৈর্ঘ্যের এবং একটি কোণ সমকোণ (90 ডিগ্রি) হয়।এর বৈশিষ্ট্যগুলি:
- - দুইটি পাশ সমান দৈর্ঘ্যের (সমদ্বিবাহু)
- - একটি কোণ সমকোণ বা 90 ডিগ্রি
- - অতিভুজ ও আয়না সমন্বয় রেখা একই রয়েছে
- - অতিভুজের উপর সোজা করে আরেকটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করা যায়
এর উপর ভিত্তি করেই এটিকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলা হয়।
সমকোণী বিষমবাহু ত্রিভুজ কাকে বলে:-
সমকোণী বিষমবাহু ত্রিভুজ সেই ত্রিভুজ যেখানে দুইটি পাশের দৈর্ঘ্য সমান নয় এবং একটি কোণ সমকোণ বা 90 ডিগ্রি।এর বৈশিষ্ট্যগুলি:
- - দুইটি পাশের দৈর্ঘ্য সমান নয় (বিষমবাহু)
- - একটি কোণ 90 ডিগ্রি বা সমকোণ
- - অতিভুজ ও আয়না সমন্বয় রেখা একই নয়
- - অতিভুজের উপর সোজা করে আরেকটি ত্রিভুজ অঙ্কন করা যায় না
সুতরাং, যেহেতু এতে দুইটি পাশের দৈর্ঘ্য সমান নয় এবং একটি কোণ সোজা কোণ, সেহেতু এটিকে সমকোণী বিষমবাহু ত্রিভুজ বলা হয়।
সমকোণী ত্রিভুজ অঙ্কন :-
সমকোণী ত্রিভুজ অঙ্কনের ধাপসমূহ:1. একটি রেখারেখক নিন এবং এর মধ্যে একটি বিন্দু নির্বাচন করুন। এটি হবে আপনার ত্রিভুজের একটি কোণাকার বিন্দু।
2. প্রথম কোণাকার বিন্দু থেকে একটি সোজা রেখা অঙ্কন করুন। এটি হবে আপনার ত্রিভুজের একটি পাশ।
3. প্রথম বিন্দু থেকে আরেকটি রেখা অঙ্কন করুন যেটি প্রথম রেখার সাথে 90 ডিগ্রি কোণ বন্ধ করবে। এটি হবে আপনার ত্রিভুজের দ্বিতীয় পাশ।
4. দুই পাশ থেকে রেখাগুলি বাড়িয়ে তৃতীয় বিন্দুতে সংযুক্ত করুন। এটি হবে আপনার ত্রিভুজের তৃতীয় কোণাকার বিন্দু।
5. তিনটি কোণাকার বিন্দু সংযুক্ত করে ত্রিভুজটি পূর্ণ করুন।
এভাবে একটি সমকোণী ত্রিভুজের অঙ্কন সম্পন্ন হয়। পাশগুলির দৈর্ঘ্য পরিবর্তন করে সমদ্বিবাহু বা বিষমবাহু ত্রিভুজ অঙ্কন করা যায়।
সমকোণী ত্রিভুজের সূত্র সমূহ :-
সমকোণী ত্রিভুজ একটি খুবই সহজ কিন্তু গুরুত্বপূর্ণ ত্রিভুজ। এর সূত্র সমূহ জানা অত্যন্ত জরুরি। সেই সাথে এর বৈশিষ্ট্য ও উপযোগিতাও অনস্বীকার্য। তাই আমি আজ সমকোণী ত্রিভুজের সূত্র সমূহ নিয়ে আলোচনা করবো।সমকোণী ত্রিভুজের এই সূত্র সমূহ অনেক গুরুত্বপূর্ণ। বিভিন্ন হিসাব-নিকাশ, ক্ষেত্রফল ইত্যাদি বের করার ক্ষেত্রে এগুলো খুবই কাজে লাগে।
সমকোণী ত্রিভুজের ক্ষেত্রফল হলো সেই ত্রিভুজের আন্তরিক এলাকার পরিমাণ।
সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র:
সমকোণী ত্রিভুজের ক্ষেত্রফল = ½ × ভূমি × উচ্চতাঅর্থাৎ,
সমকোণী ত্রিভুজের ক্ষেত্রফল = ½ × সমকোণ সংলগ্ন বাহুদ্বয়ের গুণফল
একটি উদাহরণ দেখা যাক:
ধরুন একটি সমকোণী ত্রিভুজের ভূমি হল 5 সেন্টিমিটার এবং উচ্চতা 7 সেন্টিমিটার, তাহলে সমকোণী ত্রিভুজের ক্ষেত্রফল কত?
তাহলে,
- ভূমি = 5 সেন্টিমিটার
- উচ্চতা = 7 সেন্টিমিটার
সুতরাং, ক্ষেত্রফল = ½ x 5 x 7 = 17.5 বর্গ সেন্টিমিটার।
আবার এভাবেও, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র হল:
S = (½) x b x c x sinA
এখানে,
- S = সমকোণী ত্রিভুজের ক্ষেত্রফল
- b = ত্রিভুজের একটি পাশের দৈর্ঘ্য
- c = ত্রিভুজের অপর পাশের দৈর্ঘ্য
- A = সমকোণ (90 ডিগ্রি)
সূত্রে, দুইটি পাশের দৈর্ঘ্য b ও c এর গুণফলের অর্ধেককে sin 90° দিয়ে গুণ করা হয়। যেহেতু সমকোণের sin মান 1, সুতরাং সূত্রে sinA হিসাব করা হয়না।
এই সূত্রটি ব্যবহার করে সহজেই সমকোণী ত্রিভুজের ক্ষেত্রফল বের করা যায়।
যেমন, যদি একটি সমকোণী ত্রিভুজের দুই পাশের দৈর্ঘ্য যদি 5 সেন্টিমিটার এবং 7 সেন্টিমিটার হয়, তাহলে ক্ষেত্রফল হবেঃ
S = (1/2) x 5 x 7 = 17.5 বর্গ সেন্টিমিটার
সুতরাং, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র খুবই গুরুত্বপূর্ণ এবং ব্যবহারযোগ্য।
সমকোণী ত্রিভুজের পরিসীমা কাকে বলে:
সমকোণী ত্রিভুজের পরিসীমা বলতে বোঝায় সেই ত্রিভুজের তিনটি বাহুর মোট দৈর্ঘ্য।সমকোণী ত্রিভুজে থাকে তিনটি বাহু এবং একটি ৯০ ডিগ্রির কোণ। এই তিনটি বাহুর দৈর্ঘ্যগুলোকে যোগ করলে পাওয়া যায় সমকোণী ত্রিভুজের মোট পরিসীমা।
অর্থাৎ, সমকোণী ত্রিভুজের পরিসীমা = অতিভুজ + ভূমি + উচ্চতা।
সংক্ষেপে, সমকোণী ত্রিভুজের পরিসীমা হলো সেই ত্রিভুজের তিনটি বাহুর মোট দৈর্ঘ্য।
সমকোণী ত্রিভুজের পরিসীমার সূত্র :-
সমকোণী ত্রিভুজের পরিসীমা হিসাব করার সূত্রটি হল:সমকোণী ত্রিভুজের পরিসীমা = অতিভুজ + ভূমি + উচ্চতা।
অর্থাৎ, যদি সমকোণ সংলগ্ন ভূমি দৈর্ঘ্য যদি a এবং উচ্চতা b একক এবং অতিভুজের দৈর্ঘ্য যদি c একক হয়, তাহলে পরিসীমা = a + b + c
উদাহরণস্বরূপ, যদি একটি সমকোণী ত্রিভুজের দুই বাহুর দৈর্ঘ্য যদি 4 সেন্টিমিটার এবং 6 সেন্টিমিটার এবং অতিভুজের দৈর্ঘ্য 8 সেন্টিমিটার হয়, তাহলে পরিসীমা =
a + b + c
= 4 + 6 + 8
= 18 সেন্টিমিটার
সমকোণী ত্রিভুজের অতিভুজের সূত্র :-
সমকোণী ত্রিভুজের অতিভুজের সূত্র হল:a² = b² + c² - 2bcCosA
যেখানে,
- a = অতিভুজ
- b = প্রথম পাশ
- c = দ্বিতীয় পাশ
- A = অতিভুজের সম্মুখী কোণ
এই সূত্রের ব্যাখ্যা:
সমকোণী ত্রিভুজের দুই পাশ ও একটি অতিভুজ আছে। পাশদ্বয়ের দৈর্ঘ্য যদি b ও c হয়, এবং পাশদ্বয়ের মধ্যবর্তী কোণ A হয়, তাহলে অতিভুজের দৈর্ঘ্য a হিসেবে পাওয়া যায় এই সূত্র দ্বারা।
উদাহরণ:
যদি একটি সমকোণী ত্রিভুজে,
b = 3 ইউনিট
c = 4 ইউনিট
এবং A = 60 ডিগ্রি
তাহলে,
সমকোণী ত্রিভুজের অতিভুজের সূত্রে স্থাপন করলে,
a² = 3² + 4² - 2 x 3 x 4 x cos90°
a² = 9 + 16 - 24
a² = 1
∴ a = 1 ইউনিট
অর্থাৎ উপরোক্ত তথ্য ব্যবহার করে অতিভুজের দৈর্ঘ্য 1 ইউনিট পাওয়া গেল।
সুতরাং, সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য নির্ণয় করতে এই সূত্রটি ব্যবহার করা হয়।
সমকোণী ত্রিভুজের বাহুর দৈর্ঘ্য :-
সমকোণী ত্রিভুজের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র:যদি সমকোণী ত্রিভুজে,
- প্রথম বাহুর দৈর্ঘ্য = a
- দ্বিতীয় বাহুর দৈর্ঘ্য = b
- তৃতীয় বাহুর দৈর্ঘ্য = c
তাহলে,
a² + b² = c²
অর্থাৎ প্রথম ও দ্বিতীয় বাহুর বর্গের সমষ্টি = তৃতীয় বাহুর বর্গ।
এই সূত্র ব্যবহার করে সমকোণী ত্রিভুজের যে কোন দুটি বাহুর দৈর্ঘ্য জেনে তৃতীয় বাহুর দৈর্ঘ্য বের করা যায়।
উদাহরণ:
যদি a = 3 ইউনিট এবং b = 4 ইউনিট
তাহলে,
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
অতএব, c = 5 ইউনিট
সুতরাং, তৃতীয় বাহুর দৈর্ঘ্য = 5 ইউনিট।
সমকোণী ত্রিভুজের বৈশিষ্ট্য :-
সমকোণী ত্রিভুজের কিছু গুরুত্বপূর্ণ বৈশিষ্ট্য নিম্নরূপ:
১) একটি কোণ সোজা কোণ বা ৯০ ডিগ্রির কোণ।
২) সমকোণের সম্মুখে অতিভুজ থাকে।
৩) অতিভুজ ও আয়না সমন্বয় রেখা একই হয়।
৪) সমকোণী ত্রিভুজে প্রতিটি কোণের সিনাস, কোসিনাস এবং ট্যাঞ্জেন্টের মান নির্দিষ্ট হয়।
৫) দুই ধরনের সমকোণী ত্রিভুজ রয়েছে - সমদ্বিবাহু এবং বিষমবাহু।
৬) সমদ্বিবাহু ত্রিভুজে দুই পাশ সমান। বিষমবাহুতে পাশদ্বয় সমান নয়।
৭) এর ক্ষেত্রফল বা আয়তফল সহজেই নির্ণয় করা যায়।
৮) সমকোণী ত্রিভুজে বাহুর গুণোত্তর প্রয়োগ করা যায়।
এভাবে সমকোণী ত্রিভুজের সমকোণ, অতিভুজ ও আয়না সমন্বয় রেখা, পাশের দৈর্ঘ্য ইত্যাদি বৈশিষ্ট্য রয়েছে।
উত্তর: যে ত্রিভুজে একটি কোণ ৯০ ডিগ্রি সেটি সমকোণী ত্রিভুজ বলে।
২) সমকোণী ত্রিভুজের কয় ধরন আছে?
উত্তর: ২ ধরন - সমদ্বিবাহু এবং বিষমবাহু।
৩) সমকোণী ত্রিভুজের কোন বৈশিষ্ট্য?
উত্তর: ৯০ ডিগ্রির কোণ, অতিভুজ ও আয়না সমন্বয় রেখা একই।
৪) সূক্ষ্মকোণ দ্বয়ের যোগফল কত?
উত্তর: ৯০ ডিগ্রি।
৫) সমকোণী ত্রিভুজের ক্ষেত্রফল কিভাবে বের করব?
উত্তর: অর্ধবাহুর গুণনফলের অর্ধেক।
৬) সমদ্বিবাহু ত্রিভুজ কী?
উত্তর: যেখানে দুই পাশ সমান সেটি সমদ্বিবাহু ত্রিভুজ।
৭) বিষমবাহু ত্রিভুজ কী?
উত্তর: যেখানে দুই পাশ অসমান সেটি বিষমবাহু ত্রিভুজ।
৮) সমকোণী ত্রিভুজ কিভাবে অঙ্কন করব?
উত্তর: ৯০ ডিগ্রির দুই রেখা অঙ্কন করে তৃতীয় বিন্দু দিয়ে ত্রিভুজ তৈরি করতে হবে।
৯) সমকোণী ত্রিভুজের বাহুর দৈর্ঘ্য কিভাবে বের করব?
উত্তর: বাহুর গুণোত্তর প্রয়োগ করে বাহুর দৈর্ঘ্য বের করা যায়।
১০) সমকোণী ত্রিভুজের অতিভুজের সূত্র কী?
উত্তর: a2 = b2 + c2 - 2bcCosA
১১) সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের যোগফল কত?
উত্তর: সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের যোগফল 90 ডিগ্রি।
১২) সমকোণী ত্রিভুজের কয়টি কোণ সমকোণ?
উত্তর: সমকোণী ত্রিভুজের একটি কোণ সমকোণ?
১৩) সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে কি বলে?
উত্তর: সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে বলা হয় অতিভুজ।
১) একটি কোণ সোজা কোণ বা ৯০ ডিগ্রির কোণ।
২) সমকোণের সম্মুখে অতিভুজ থাকে।
৩) অতিভুজ ও আয়না সমন্বয় রেখা একই হয়।
৪) সমকোণী ত্রিভুজে প্রতিটি কোণের সিনাস, কোসিনাস এবং ট্যাঞ্জেন্টের মান নির্দিষ্ট হয়।
৫) দুই ধরনের সমকোণী ত্রিভুজ রয়েছে - সমদ্বিবাহু এবং বিষমবাহু।
৬) সমদ্বিবাহু ত্রিভুজে দুই পাশ সমান। বিষমবাহুতে পাশদ্বয় সমান নয়।
৭) এর ক্ষেত্রফল বা আয়তফল সহজেই নির্ণয় করা যায়।
৮) সমকোণী ত্রিভুজে বাহুর গুণোত্তর প্রয়োগ করা যায়।
এভাবে সমকোণী ত্রিভুজের সমকোণ, অতিভুজ ও আয়না সমন্বয় রেখা, পাশের দৈর্ঘ্য ইত্যাদি বৈশিষ্ট্য রয়েছে।
সমকোণী ত্রিভুজ সম্পর্কে FAQ এর কিছু প্রশ্নোত্তর:
১) সমকোণী ত্রিভুজ বলতে কি বুঝায়?উত্তর: যে ত্রিভুজে একটি কোণ ৯০ ডিগ্রি সেটি সমকোণী ত্রিভুজ বলে।
২) সমকোণী ত্রিভুজের কয় ধরন আছে?
উত্তর: ২ ধরন - সমদ্বিবাহু এবং বিষমবাহু।
৩) সমকোণী ত্রিভুজের কোন বৈশিষ্ট্য?
উত্তর: ৯০ ডিগ্রির কোণ, অতিভুজ ও আয়না সমন্বয় রেখা একই।
৪) সূক্ষ্মকোণ দ্বয়ের যোগফল কত?
উত্তর: ৯০ ডিগ্রি।
৫) সমকোণী ত্রিভুজের ক্ষেত্রফল কিভাবে বের করব?
উত্তর: অর্ধবাহুর গুণনফলের অর্ধেক।
৬) সমদ্বিবাহু ত্রিভুজ কী?
উত্তর: যেখানে দুই পাশ সমান সেটি সমদ্বিবাহু ত্রিভুজ।
৭) বিষমবাহু ত্রিভুজ কী?
উত্তর: যেখানে দুই পাশ অসমান সেটি বিষমবাহু ত্রিভুজ।
৮) সমকোণী ত্রিভুজ কিভাবে অঙ্কন করব?
উত্তর: ৯০ ডিগ্রির দুই রেখা অঙ্কন করে তৃতীয় বিন্দু দিয়ে ত্রিভুজ তৈরি করতে হবে।
৯) সমকোণী ত্রিভুজের বাহুর দৈর্ঘ্য কিভাবে বের করব?
উত্তর: বাহুর গুণোত্তর প্রয়োগ করে বাহুর দৈর্ঘ্য বের করা যায়।
১০) সমকোণী ত্রিভুজের অতিভুজের সূত্র কী?
উত্তর: a2 = b2 + c2 - 2bcCosA
১১) সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের যোগফল কত?
উত্তর: সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের যোগফল 90 ডিগ্রি।
১২) সমকোণী ত্রিভুজের কয়টি কোণ সমকোণ?
উত্তর: সমকোণী ত্রিভুজের একটি কোণ সমকোণ?
১৩) সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে কি বলে?
উত্তর: সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে বলা হয় অতিভুজ।








0 মন্তব্যসমূহ
Please do not enter any spam link in the comment box.