সন্নিহিত কোণ কাকে বলে? উদাহরণ? সন্নিহিত কোণ এর বৈশিষ্ট্য?

সন্নিহিত কোণ সম্পর্কে ভূমিকা বা সূচনা:

জ্যামিতিতে কোণ অত্যন্ত গুরুত্বপূর্ণ ধারণা। কোণ হল দুটি রেখার মধ্যে সৃষ্ট হওয়া স্থান। কোণের দুটি প্রধান উপাদান রয়েছে - শীর্ষবিন্দু এবং কোণরেখা। কোণরেখা দুটি কোণাংশের সীমারেখা। যখন দুটি কোণের একই শীর্ষবিন্দু থাকে এবং কোণরেখা একই হয়, তখন ঐ দুটি কোণকে সন্নিহিত বা সমকোণ বলা হয়।

অর্থাৎ যখন কোণদ্বয়ের পরিমাণ একই হয়, তখন তাকে সন্নিহিত বলা হয়। সন্নিহিত কোণ নিয়ে আলোচনা করা জ্যামিতিতে খুবই গুরুত্বপূর্ণ।

সন্নিহিত কোণগুলি জ্যামিতির একটি মৌলিক ধারণা, তবে সেগুলি শুধুমাত্র গণিতের পাঠ্যপুস্তক এবং সমস্যার মধ্যে সীমাবদ্ধ নয়। এই কোণগুলি দৈনন্দিন জীবনে আমাদের চারপাশে, ভবনের কোণ থেকে ছবির ফ্রেম পর্যন্ত পাওয়া যায়।

সন্নিহিত কোণগুলিকে দুটি কোণ হিসাবে সংজ্ঞায়িত করা হয় যা একটি সাধারণ শীর্ষ এবং একটি সাধারণ দিক ভাগ করে কিন্তু ওভারল্যাপ করে না। এগুলি বিস্তৃত বস্তু এবং স্থানগুলিতে পাওয়া যেতে পারে এবং সেগুলি বোঝা আমাদের চারপাশের বিশ্বকে আরও ভালভাবে বুঝতে সাহায্য করতে পারে।

আরও পড়ুনঃ কোণ কাকে বলে?

এই ব্লগে, আমরা আপনাকে এই ধারণাটিকে আরও ভালভাবে উপলব্ধি করতে সাহায্য করার জন্য সন্নিহিত কোণ কাকে বলে, এর বৈশিষ্ট্য এবং কিছু বাস্তব-জীবনের উদাহরণ দেখব।

বিল্ডিং এর কোণ থেকে রাস্তার মোড় পর্যন্ত, আমরা আমাদের দৈনন্দিন জীবনে সন্নিহিত কোণগুলি বিদ্যমান বিভিন্ন উপায়ে অন্বেষণ করব।

সুতরাং, এই অপরিহার্য ধারণা সম্পর্কে আপনার বোধগম্যতা প্রসারিত করার জন্য প্রস্তুত হন এবং আপনার দৈনন্দিন পরিবেশে সন্নিহিত কোণগুলি কীভাবে চিহ্নিত করবেন তা শিখুন।

সন্নিহিত কোণ কাকে বলে :-

যদি সমতলে দুইটি কোণের একই শীর্ষবিন্দু হয় ও তাদের একটি সাধারণ রশ্মি থাকে এবং কোণায় সাধারণ রশ্মির বিপরীত পাশে অবস্থান করে, তবে ঐ কোণদ্বয়কে সন্নিহিত কোণ বলে।

অন্যভাবে বললে, যদি দুটি কোণের একই শীর্ষবিন্দু থাকে এবং একটি সাধারণ রেখা থাকে যা উভয় কোণকে বিভক্ত করে, তবে ঐ দুটি কোণকে সন্নিহিত বা সমকোণ বলা হয়।

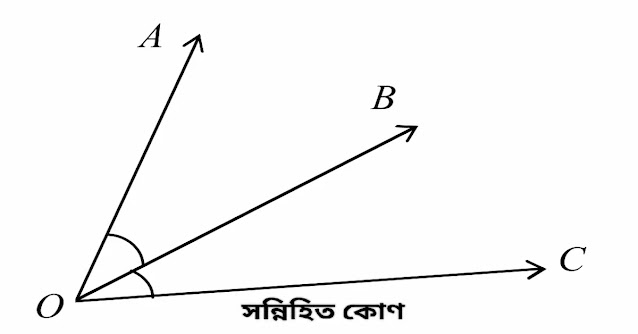
নীচের চিত্রে, O বিন্দুটি <AOB ও <BOC এর শীর্ষবিন্দু। O বিন্দু <AOB ও <BOC উৎপন্নকারী রশ্মিগুলোর মধ্যে OB সাধারণ রশ্মি । কোণ দুইটি সাধারণ রশ্মি OB এর বিপরীত পাশে অবস্থিত। <AOB ও <BOC পরস্পর সন্নিহিত কোণ। সন্নিহিত কোণদ্বয়ের একই শীর্ষবিন্দু O এবং একটি সাধারণ বাহু OB। OA এবং OC কোণ দুইটির বহিঃস্থ বাহু।

সন্নিহিত কোণের বৈশিষ্ট্য :-

১. ষসন্নিহিত কোণগুলি একটি সাধারণ দিক বা সাধারণ বাহু (common side/arm) ভাগ করে।

কোনও কোণের দিক বা বাহু হল কোণরেখার দুই অংশ।

যেহেতু সন্নিহিত কোণগুলি একই পরিমাণের, তাদের দিক বা বাহুও একই হয়। একই সাধারণ দিক বা বাহু ভাগ করাটি সন্নিহিত কোণের একটি প্রধান বৈশিষ্ট্য।

২. সন্নিহিত কোণগুলি একটি সাধারণ শীর্ষবিন্দু (common vertex) ভাগ করে।

কোনও কোণের শীর্ষবিন্দু হল সেই বিন্দু যেটিতে কোণের দুই কোণাংশ মিলে যায়।

যেহেতু সন্নিহিত কোণগুলি একই পরিমাণের, তাদের শীর্ষবিন্দুও একই হয়। একই শীর্ষবিন্দু ভাগ করা সন্নিহিত কোণের একটি প্রধান বৈশিষ্ট্য।

৩. সন্নিহিত কোণগুলি ওভারল্যাপ করে না - এটি সন্নিহিত কোণের একটি গুরুত্বপূর্ণ বৈশিষ্ট্য।

ওভারল্যাপ করা মানে দুটি কোণ একে অপরকে আংশিকভাবে আচ্ছাদন করে। কিন্তু সন্নিহিত কোণগুলি একই পরিমাণের হওয়ায়, তাই কোনও ওভারল্যাপ ঘটে না।

 
আরও পড়ুনঃ অন্তঃস্থ কোণ কাকে বলে?

উদাহরণস্বরূপ, 60 ডিগ্রির দুটি সন্নিহিত কোণ ধরুন। এগুলি 60 ডিগ্রি জুড়ে সম্পূর্ণরূপে স্থান দেবে, কোনও ওভারল্যাপ ছাড়াই। সুতরাং ওভারল্যাপ না করাটি সন্নিহিত কোণের একটি অনিবার্য বৈশিষ্ট্য।

৪. সন্নিহিত কোণগুলির সাধারণ বাহুর উভয় পাশে একটি অ-সাধারণ বাহু রয়েছে।

এটি সন্নিহিত কোণের একটি গুরুত্বপূর্ণ বৈশিষ্ট্য।

সন্নিহিত কোণগুলি একটি সাধারণ বাহু (common arm) দ্বারা ভাগ করা হয়। এই সাধারণ বাহুর উভয় পাশে থাকে দুটি অ-সাধারণ বাহু (non-common arms)।

উদাহরণস্বরূপ, 60 ডিগ্রির দুটি সন্নিহিত কোণ ধরুন। এর সাধারণ বাহু হ'ল 60 ডিগ্রির কোণরেখা। এই সাধারণ বাহুর উভয় পাশে থাকবে দুটি 30 ডিগ্রির অ-সাধারণ বাহু।

সুতরাং, সন্নিহিত কোণে সাধারণ বাহুর উভয় পাশে অ-সাধারণ বাহু থাকা একটি নির্ধারিত বৈশিষ্ট্য।

৫. সন্নিহিত কোণগুলির একটি সাধারণ অভ্যন্তরীণ বিন্দু থাকে না।

কোনও কোণের অভ্যন্তরীণ বিন্দু হল যেটি কোণরেখার মধ্যে অবস্থিত এবং কোণের দুই কোণাংশের থেকে সমান দূরত্বে রয়েছে।

কিন্তু যেহেতু সন্নিহিত কোণগুলি একই পরিমাণের, তাই কোনও একটি নির্দিষ্ট বিন্দু থাকে না যেটি দুই কোণাংশ থেকে সমান দূরত্বে থাকবে।

উদাহরণস্বরূপ, যদি আপনি 60 ডিগ্রির দুটি সন্নিহিত কোণ নিয়ে থাকেন, তাহলে কোনও একটি বিন্দু কোণাংশ দুটির থেকে সমান দূরত্বে থাকবে না। সুতরাং, সন্নিহিত কোণে একটি সাধারণ অভ্যন্তরীণ বিন্দু অনুপস্থিত থাকে।

এটি সন্নিহিত কোণের একটি গুরুত্বপূর্ণ বৈশিষ্ট্য যা একে অ-সন্নিহিত কোণ থেকে পৃথক করে।

আশা করি সন্নিহিত কোণের বৈশিষ্ট্য স্পষ্ট করে দিয়েছে!

সন্নিহিত কোণগুলি সনাক্ত করার কিছু উপায়:

• - যদি দুটি কোণের একই শীর্ষবিন্দু থাকে, তাহলে তারা সন্নিহিত কোণ হতে পারে।
• - যদি দুটি কোণের একই সাধারণ দিক বা বাহু থাকে, তাহলে তারা সন্নিহিত কোণ হতে পারে।
• - যদি দুটি কোণ একে অপরকে আংশিকভাবে আচ্ছাদন না করে, তাহলে তারা সন্নিহিত কোণ হতে পারে।
• - যদি দুটি কোণের কোন সাধারণ অভ্যন্তরীণ বিন্দু না থাকে, তাহলে তারা সন্নিহিত কোণ হতে পারে।
• - কোণরেখার মাপ দিয়ে দেখা যে দুটি কোণের পরিমাণ একই কিনা। যদি একই হয়, তাহলে তারা সন্নিহিত।
• - জ্যামিতিক সাবস্ট্রাকশন ব্যবহার করে দেখা যায় কোণগুলি কি সন্নিহিত কি না।

আরও পড়ুনঃ প্রবৃদ্ধ কোণ কাকে বলে?

সন্নিহিত কোণের উদাহরণ :-

আমরা আমাদের পরিবেশে আমাদের চারপাশে সন্নিহিত কোণের অনেক বাস্তব-জীবনের উদাহরণ দেখতে পারি। এখানে আপনার জন্য কয়েকটি উদাহরণ রয়েছে:

বিমানের ডানা :-

বিমানের ডানা একটি ভাল সন্নিহিত কোণের উদাহরণ।

বিমানের প্রতিটি ডানা দুটি সমান্তরাল প্রস্থের সঙ্গে সংযুক্ত থাকে, যা একটি সাধারণ বাহু তৈরি করে। এই সাধারণ বাহুর দুই পাশে থাকে দুটি ডানা, যা ক্রমাগত অ-সাধারণ বাহু।

প্রতিটি ডানার শীর্ষবিন্দু বিমানের শরীরে একই বিন্দুতে সংযুক্ত থাকে। ডানাগুলি একে অপরকে আংশিকভাবে আচ্ছাদন করে না।

সুতরাং, একটি বিমানের ডানা সন্নিহিত কোণের একটি ভাল বাস্তব জীবনের উদাহরণ।

বইয়ের পাতা :-

যেহেতু সাধারণত বইয়ের পৃষ্ঠাগুলি 90 ডিগ্রিতে মোড় হয়, তাই পৃষ্ঠার দুই পাশের কোণগুলি সন্নিহিত কোণের মতো।

এছাড়াও, পৃষ্ঠার উপরের ও নিচের কোণগুলিও 90 ডিগ্রিতে মোড় হয়, যা সন্নিহিত কোণ তৈরি করে।

পৃষ্ঠার চারপাশের কোণগুলি একই সাধারণ বাইন্ডিং ব্যবহার করে এবং ওভারল্যাপ করে না।

সুতরাং, একটি বইয়ের পৃষ্ঠা সন্নিহিত কোণের একটি ভালো উদাহরণ।

কুমিরের খোলা মুখ :

একটি কুমিরের মুখ খোলা অবস্থায় সন্নিহিত কোণের একটি উদাহরণ হিসাবে ব্যবহার করা যায়।

যেহেতু কুমিরের মুখের দুই পাশ সমান্তরাল রয়েছে, তাই সেগুলি মিলে একটি সাধারণ বাহু তৈরি করে। এর উভয় পাশে রয়েছে কুমিরের মুখের দুটি অংশ, যা অ-সাধারণ বাহু।

কুমিরের মুখের দুই কোণ মিলে একটি সাধারণ শীর্ষবিন্দু তৈরি করে এবং কোনও ওভারল্যাপ করে না।

সুতরাং, একটি মুখ খোলা কুমিরের মুখ সন্নিহিত কোণের একটি ভালো উদাহরণ।

দরজার কোণ:

দরজার কোণ সাধারণত সন্নিহিত কোণের একটি উদাহরণ হিসাবে বিবেচিত হয়।

কারণ:

- দরজার দুই পাশের কোণগুলি সাধারণত 90 ডিগ্রি হয়, যা সন্নিহিত কোণের মতো।
- উভয় পাশের কোণগুলি একই সাধারণ দিক ভাগ করে এবং ওভারল্যাপ করে না।
- দরজার দুই পাশের কোণগুলির একই সাধারণ শীর্ষবিন্দু রয়েছে।
- দরজার কোণগুলির মধ্যে কোন সাধারণ অভ্যন্তরীণ বিন্দু নেই।

সুতরাং, দরজার কোণ সন্নিহিত কোণের স্পষ্ট একটি উদাহরণ।

আঙ্গুলের মধ্যে কোণ:

আপনার আঙ্গুলের মধ্যে কোণগুলি সন্নিহিত কোণের একটি উদাহরণ হিসাবে বিবেচনা করা যেতে পারে।

কারণ:

- আঙ্গুল মোড়ানোর সময় আঙ্গুলের দুই পাশের মধ্যে কোণগুলি সাধারণত সমান হয়।
- উভয় পাশের কোণগুলির একই সাধারণ শীর্ষবিন্দু রয়েছে যেখানে আঙ্গুল মোড়ানো হয়।
- কোণগুলি একই সাধারণ দিক বা বাহু ভাগ করে।
- কোণগুলি পরস্পরের সাথে ওভারল্যাপ করে না।
- কোন সাধারণ অভ্যন্তরীণ বিন্দু নেই।

সুতরাং, আঙ্গুলের মধ্যে কোণ সন্নিহিত কোণের ধারণাকে প্রতিনিধিত্ব করে।

খোলা কাঁচি এর ব্লেড:

একটি খোলা কাঁচির ব্লেড সন্নিহিত কোণের একটি উদাহরণ হিসাবে বিবেচনা করা যেতে পারে।

কারণ:

- কাঁচির ব্লেডের দুই পাশ সমান্তরাল রয়েছে, যা একটি সাধারণ বাহু তৈরি করে।
- ব্লেডের দুই পাশ একই সাধারণ শীর্ষবিন্দুতে মিলেছে যেখানে ব্লেডটি মোড়ানো হয়েছে।
- ব্লেডের উভয় পাশের কোণগুলি পরস্পরের সাথে ওভারল্যাপ করে না।
- কোন সাধারণ অভ্যন্তরীণ বিন্দু নেই।
- উভয় পাশের কোণগুলি সমান।

সুতরাং, খোলা কাঁচির ব্লেড সন্নিহিত কোণের একটি উদাহরণ।

আরও পড়ুনঃ অনুরূপ কোণ কাকে বলে?

সিঁড়ি:

সিঁড়ির ধাপগুলি সন্নিহিত কোণের একটি উদাহরণ হিসাবে বিবেচনা করা যেতে পারে।

কারণ:

- প্রতিটি সিঁড়ির ধাপ 90 ডিগ্রিতে মোড়ানো থাকে, যা সন্নিহিত কোণ তৈরি করে।
- ধাপগুলি একই সাধারণ বাহু বা পাশ ভাগ করে যেখান দিয়ে সিঁড়িটি সংযুক্ত হয়েছে।
- প্রতিটি ধাপের কোণগুলির একই সাধারণ শীর্ষবিন্দু আছে।
- ধাপগুলি পরস্পরের সাথে ওভারল্যাপ করে না।
- কোন সাধারণ অভ্যন্তরীণ বিন্দু নেই।

সুতরাং, সিঁড়ির ধাপগুলি সন্নিহিত কোণের একটি উদাহরণ।