সমকোণ জ্যামিতির একটি গুরুত্বপূর্ণ ধারণা, এবং স্থাপত্য, প্রকৌশল এবং পদার্থবিদ্যা সহ বিভিন্ন ক্ষেত্রে ব্যাপকভাবে ব্যবহৃত হয়। এই নিবন্ধে, আমরা সমকোণ কাকে বলে, এর উদাহরণ, সমকোণগুলির বৈশিষ্ট্য এবং ব্যবহারগুলি আলোচনা করব৷
আরও সহজ ভাবে বললে, একটি সরল কোণের সমদ্বিখন্ডককে লম্ব এবং সংশ্লিষ্ট সন্নিহিত কোণের প্রত্যেকটিকে সমকোণ বলে।
চিত্রে, < AOB সরল কোণকে O বিন্দুতে OC রশ্মি দ্বারা সমদ্বিখণ্ডিত করা হয়েছে। এর ফলে <BOC & <COA সন্নিহিত কোণ দুইটির প্রত্যেকেই সমকোণ এবং এদের ডিগ্রি পরিমাপ 90°। OB রশ্মি ও তার বিপরীত রশ্মি OA উভয়ের উপর OC রশ্মি লম্ব। OC রশ্মিকে AB রেখার উপর O বিন্দুতে লম্ব বলা হয়।
একটি কোণের ডিগ্রি পরিমাণ 90° হলে তাকে সমকোণ বলা হয়। দুই সমকোণ একত্রে একটি সরলকোণ উৎপন্ন করে।
অর্থাৎ একটি 90-ডিগ্রী কোণ সর্বদা একটি সমকোণ। একটি তীব্র কোণ হল একটি যা 90 ডিগ্রির কম, যখন একটি স্থূল কোণ হল একটি যা 90 ডিগ্রির বেশি।
আরও পড়ুনঃ সন্নিহিত কোণ কাকে বলে?
কোনো রেখাংশের লম্ব-বিত্তক দ্বারা উৎপন্ন সন্নিহিত কোণ দুইটি প্রত্যেকে সমকোণ।
রেডিয়ানে সমকোণ π/2 হিসাবে উপস্থাপিত হয়। একটি সমকোণের আকৃতি দেখতে L বর্ণমালার মতো।
নির্মাণ: বিল্ডিং এবং অন্যান্য কাঠামো বর্গাকার এবং সমতল হয় তা নিশ্চিত করার জন্য সঠিক কোণ অপরিহার্য। নির্মাতারা সঠিক কোণ তৈরি করতে এবং সবকিছু সঠিক অবস্থানে রয়েছে তা নিশ্চিত করতে ছুতারের স্কোয়ার এবং স্পিরিট লেভেলের মতো টুল ব্যবহার করেন।
গণিত: সমকোণ জ্যামিতি এবং ত্রিকোণমিতির একটি গুরুত্বপূর্ণ অংশ। এগুলি কোণ এবং দূরত্ব গণনা করা থেকে শুরু করে সমকোণী ত্রিভুজের কর্ণ খুঁজে বের করা পর্যন্ত সবকিছুতে ব্যবহৃত হয়।
ন্যাভিগেশন: ন্যাভিগেশন এবং ম্যাপিং এ ডান কোণগুলি একটি রেফারেন্স পয়েন্ট হিসাবে ব্যবহৃত হয়।
উদাহরণস্বরূপ, নাবিকরা তাদের অক্ষাংশ নির্ধারণ করতে উত্তর নক্ষত্র ব্যবহার করে, যার জন্য তাদের আকাশে একটি সমকোণ সনাক্ত করতে হয়।
ফটোগ্রাফি: আকর্ষণীয় রচনা এবং দৃষ্টিভঙ্গি তৈরি করতে ফটোগ্রাফিতে প্রায়ই ডান কোণ ব্যবহার করা হয়। ফটোগ্রাফাররা একটি সমকোণ ভিউফাইন্ডার বা ট্রাইপড ব্যবহার করতে পারেন যাতে তাদের ক্যামেরা সমতল এবং সোজা হয়।
শিল্প এবং নকশা: সমকোণগুলি শিল্প এবং নকশার একটি মূল উপাদান। তারা পেইন্টিং এবং ভাস্কর্য থেকে আসবাবপত্র এবং ফ্যাশন সবকিছুর মধ্যে দৃষ্টিকোণ, ভারসাম্য এবং প্রতিসাম্য তৈরি করতে ব্যবহৃত হয়।
উপসংহারে, সমকোণগুলি জ্যামিতির একটি অপরিহার্য ধারণা যার বিস্তৃত বৈশিষ্ট্য এবং ব্যবহার রয়েছে।
একটি দরজার প্রান্তে সমকোণের একটি উদাহরণ হতে পারে:
যেখানে দরজার প্রান্ত দুইটি ভাগে ভাগ করা আছে - একটি অংশ দেয়ালের সাথে এবং অন্যটি দরজার সাথে সংযুক্ত। দেয়াল এবং দরজার মধ্যে যে কোণটি তৈরি হয়, সেটি একটি সমকোণ।
কারণ, এই কোণটি ৯০ ডিগ্রির এবং দুই প্রস্থ সমান্তরাল এবং সমদৈর্ঘ্য।
অর্থাৎ এটি একটি সমকোণের সকল উপাদান পূরণ করে। সুতরাং এটি দরজার প্রান্তে সমকোণের একটি ভাল উদাহরণ।
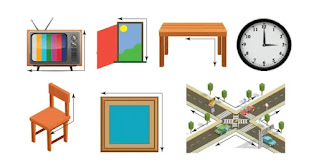
টেলিভিশনের চার প্রান্ত :
একটি টেলিভিশনের চার প্রান্তে সমকোণের উদাহরণ হতে পারে:
1. ডান প্রান্ত এবং উপরের প্রান্তের মধ্যে যে কোণ তৈরি হয় তা একটি সমকোণ।
2. বাম প্রান্ত এবং নিচের প্রান্তের মধ্যে যে কোণ তৈরি হয় তাও একটি সমকোণ।
3. ডান প্রান্ত এবং নিচের প্রান্তের মধ্যে যে কোণ তৈরি হয় তা আবারো সমকোণ।
4. বাম প্রান্ত এবং উপরের প্রান্তের মধ্যে যে কোণ তাও সমকোণ।
কারণ এসব কোণের পরিমাপ ৯০ ডিগ্রি এবং প্রস্থগুলো সমান্তরাল ও সমদৈর্ঘ্য।
আরও পড়ুনঃ ত্রিভুজ কাকে বলে?
চেয়ারের কোণ :
চেয়ারের কোণ একটি উদাহরণ সমকোণের জন্য দেওয়া যেতে পারে:
সুতরাং চেয়ারে অনেক সমকোণের উদাহরণ রয়েছে।
সমকোণ কাকে বলে:-
একটি সরল রেখা যদি অপর একটি সরল রেখার উপর দণ্ডায়মান হয় যে ঐ সরল রেখার উভয় পার্শ্বস্থ সন্নিহিত কোণ দুইটি পরস্পর সমান, তবে তাদের প্রত্যেক কোণকে সমকোণ বলে।আরও সহজ ভাবে বললে, একটি সরল কোণের সমদ্বিখন্ডককে লম্ব এবং সংশ্লিষ্ট সন্নিহিত কোণের প্রত্যেকটিকে সমকোণ বলে।
চিত্রে, < AOB সরল কোণকে O বিন্দুতে OC রশ্মি দ্বারা সমদ্বিখণ্ডিত করা হয়েছে। এর ফলে <BOC & <COA সন্নিহিত কোণ দুইটির প্রত্যেকেই সমকোণ এবং এদের ডিগ্রি পরিমাপ 90°। OB রশ্মি ও তার বিপরীত রশ্মি OA উভয়ের উপর OC রশ্মি লম্ব। OC রশ্মিকে AB রেখার উপর O বিন্দুতে লম্ব বলা হয়।
একটি কোণের ডিগ্রি পরিমাণ 90° হলে তাকে সমকোণ বলা হয়। দুই সমকোণ একত্রে একটি সরলকোণ উৎপন্ন করে।
অর্থাৎ একটি 90-ডিগ্রী কোণ সর্বদা একটি সমকোণ। একটি তীব্র কোণ হল একটি যা 90 ডিগ্রির কম, যখন একটি স্থূল কোণ হল একটি যা 90 ডিগ্রির বেশি।
আরও পড়ুনঃ সন্নিহিত কোণ কাকে বলে?
কোনো রেখাংশের লম্ব-বিত্তক দ্বারা উৎপন্ন সন্নিহিত কোণ দুইটি প্রত্যেকে সমকোণ।
রেডিয়ানে সমকোণ π/2 হিসাবে উপস্থাপিত হয়। একটি সমকোণের আকৃতি দেখতে L বর্ণমালার মতো।
সমকোণ এর বৈশিষ্ট্য :-
- যে কোণটির দুই প্রস্থ সমান্তরাল এবং সমদৈর্ঘ্য, সেই কোণটির কোণমাপ অবশ্যই ৯০ ডিগ্রি হবে। অর্থাৎ সমকোণের মান অবশ্যই ৯০ ডিগ্রি হবে।
- ১ সমকোণ = ৯০ ডিগ্রি = ১/৪ অংশ বৃত্তাকার = ১০০ গ্রেডিয়ানের সমান।
- সমকোণগুলি সাধারণত কোণের শীর্ষে একটি ছোট বর্গ দ্বারা উপস্থাপিত হয়।
- একটি সমকোণ দ্বিখণ্ডক কোণটিকে দুটি সমান অংশে বিভক্ত করে, প্রতিটি 45 ডিগ্রি পরিমাপ করে।
- বর্গাকার এবং আয়তক্ষেত্র থেকে ত্রিভুজ এবং ট্র্যাপিজয়েড পর্যন্ত সমস্ত ধরণের আকার এবং চিত্রে সমকোণ পাওয়া যায়।
- সমকোণের পরস্পর দুই টি লম্ব বাহু থাকে।
- একটি বর্গক্ষেত্রের বাহুগুলো সব সমকোণ।
- একটি বর্গক্ষেত্রের কর্ণ সমকোণে ছেদ করে।
- সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহু বৃহত্তম।
- একটি ত্রিভুজের উচ্চতা যা তার ভিত্তির সাথে লম্ব একটি সমকোণ তৈরি করে।
- সমকোণগুলি ইউক্লিডীয় জ্যামিতির জন্য মৌলিক বলে বিবেচিত হয়।
- ত্রিকোণমিতিতে সমকোণ একটি গুরুত্বপূর্ণ ভূমিকা পালন করে।
সমকোণের ব্যবহার :-
এই বৈশিষ্ট্যগুলিকে মাথায় রেখে, আসুন সমকোণগুলির সবচেয়ে সাধারণ ব্যবহারগুলির কিছু দেখে নেওয়া যাক।নির্মাণ: বিল্ডিং এবং অন্যান্য কাঠামো বর্গাকার এবং সমতল হয় তা নিশ্চিত করার জন্য সঠিক কোণ অপরিহার্য। নির্মাতারা সঠিক কোণ তৈরি করতে এবং সবকিছু সঠিক অবস্থানে রয়েছে তা নিশ্চিত করতে ছুতারের স্কোয়ার এবং স্পিরিট লেভেলের মতো টুল ব্যবহার করেন।
গণিত: সমকোণ জ্যামিতি এবং ত্রিকোণমিতির একটি গুরুত্বপূর্ণ অংশ। এগুলি কোণ এবং দূরত্ব গণনা করা থেকে শুরু করে সমকোণী ত্রিভুজের কর্ণ খুঁজে বের করা পর্যন্ত সবকিছুতে ব্যবহৃত হয়।
ন্যাভিগেশন: ন্যাভিগেশন এবং ম্যাপিং এ ডান কোণগুলি একটি রেফারেন্স পয়েন্ট হিসাবে ব্যবহৃত হয়।
উদাহরণস্বরূপ, নাবিকরা তাদের অক্ষাংশ নির্ধারণ করতে উত্তর নক্ষত্র ব্যবহার করে, যার জন্য তাদের আকাশে একটি সমকোণ সনাক্ত করতে হয়।
আরও পড়ুনঃ কোণ কাকে বলে?
ফটোগ্রাফি: আকর্ষণীয় রচনা এবং দৃষ্টিভঙ্গি তৈরি করতে ফটোগ্রাফিতে প্রায়ই ডান কোণ ব্যবহার করা হয়। ফটোগ্রাফাররা একটি সমকোণ ভিউফাইন্ডার বা ট্রাইপড ব্যবহার করতে পারেন যাতে তাদের ক্যামেরা সমতল এবং সোজা হয়।
শিল্প এবং নকশা: সমকোণগুলি শিল্প এবং নকশার একটি মূল উপাদান। তারা পেইন্টিং এবং ভাস্কর্য থেকে আসবাবপত্র এবং ফ্যাশন সবকিছুর মধ্যে দৃষ্টিকোণ, ভারসাম্য এবং প্রতিসাম্য তৈরি করতে ব্যবহৃত হয়।
উপসংহারে, সমকোণগুলি জ্যামিতির একটি অপরিহার্য ধারণা যার বিস্তৃত বৈশিষ্ট্য এবং ব্যবহার রয়েছে।
সমকোণের উদাহরণ :-
দরজার প্রান্ত :একটি দরজার প্রান্তে সমকোণের একটি উদাহরণ হতে পারে:
যেখানে দরজার প্রান্ত দুইটি ভাগে ভাগ করা আছে - একটি অংশ দেয়ালের সাথে এবং অন্যটি দরজার সাথে সংযুক্ত। দেয়াল এবং দরজার মধ্যে যে কোণটি তৈরি হয়, সেটি একটি সমকোণ।
কারণ, এই কোণটি ৯০ ডিগ্রির এবং দুই প্রস্থ সমান্তরাল এবং সমদৈর্ঘ্য।
অর্থাৎ এটি একটি সমকোণের সকল উপাদান পূরণ করে। সুতরাং এটি দরজার প্রান্তে সমকোণের একটি ভাল উদাহরণ।
টেলিভিশনের চার প্রান্ত :
একটি টেলিভিশনের চার প্রান্তে সমকোণের উদাহরণ হতে পারে:
1. ডান প্রান্ত এবং উপরের প্রান্তের মধ্যে যে কোণ তৈরি হয় তা একটি সমকোণ।
2. বাম প্রান্ত এবং নিচের প্রান্তের মধ্যে যে কোণ তৈরি হয় তাও একটি সমকোণ।
3. ডান প্রান্ত এবং নিচের প্রান্তের মধ্যে যে কোণ তৈরি হয় তা আবারো সমকোণ।
4. বাম প্রান্ত এবং উপরের প্রান্তের মধ্যে যে কোণ তাও সমকোণ।
কারণ এসব কোণের পরিমাপ ৯০ ডিগ্রি এবং প্রস্থগুলো সমান্তরাল ও সমদৈর্ঘ্য।
আরও পড়ুনঃ ত্রিভুজ কাকে বলে?
চেয়ারের কোণ :
চেয়ারের কোণ একটি উদাহরণ সমকোণের জন্য দেওয়া যেতে পারে:
- - চেয়ারের সিট এবং ব্যাকের মধ্যে যে কোণ তৈরি হয়, তা একটি সমকোণ। এখানে দুই প্রস্থ সমান্তরাল এবং সমদৈর্ঘ্য, এবং কোণমাপ ৯০ ডিগ্রি।
- - চেয়ারের সিট এবং পায়ের মধ্যে যে কোণ তৈরি হয়, সেটিও একটি সমকোণ। এখানেও প্রস্থগুলো সমান্তরাল ও সমদৈর্ঘ্য এবং কোণমাপ ৯০ ডিগ্রি।
- - চেয়ারের ব্যাক এবং পায়ের মধ্যে কোণটিও সমকোণ।
সুতরাং চেয়ারে অনেক সমকোণের উদাহরণ রয়েছে।









0 মন্তব্যসমূহ
Please do not enter any spam link in the comment box.