প্রিয় পাঠকগণ, আজকে আমি আপনাদের সাথে শেয়ার করতে চলেছি জ্যামিতির একটি খুবই গুরুত্বপূর্ণ ধারণা - সামান্তরিক কাকে বলে, এর বৈশিষ্ট্য, উদাহরণ ও ব্যবহার সম্পর্কে।
জ্যামিতিতে দুটি রেখা বা দুটি বাহু যখন পরস্পর সমান্তরাল এবং সমপরিমাপের হয়, তখন তাদের মধ্যে সামান্তরিক সম্পর্ক বলে। এই সামান্তরিকতা নিয়ে আজ আমরা বিস্তারিত আলোচনা করব।
সামান্তরিক বা প্যারালেল লাইনস নিয়ে জেনে নেওয়া খুবই গুরুত্বপূর্ণ, কারণ এর ব্যবহার ঘটে জ্যামিতি, ট্রিগনোমেট্রি, ভৌতবিজ্ঞান এবং অন্যান্য বিষয়ে। তাই আমাদের জন্য এটি শেখা খুবই জরুরি। আসুন আজ আমরা সামান্তরিক সম্পর্কে গভীরভাবে জেনে নিই।
আশা করি এই পোস্ট আপনাদের কাজে লাগবে। এই বিষয়ে যে কোন প্রশ্ন থাকলে কমেন্ট করে জানাতে পারেন।
সামান্তরিক (Parallelogram) শব্দটি এসেছে গ্রীক ভাষার 'প্যারালেলোগ্রামন' থেকে। যার অর্থ "সমান্তরাল রেখার দ্বারা ঘিরে ধরা"। সামান্তরিক হলো একটি বিশেষ ধরনের চতুর্ভুজ যেখানে বিপরীত দুই বাহু একে অপরকে সমান্তরাল এবং সমান দৈর্ঘ্যের।
জ্যামিতিতে দুটি রেখা বা দুটি বাহু যখন পরস্পর সমান্তরাল এবং সমপরিমাপের হয়, তখন তাদের মধ্যে সামান্তরিক সম্পর্ক বলে। এই সামান্তরিকতা নিয়ে আজ আমরা বিস্তারিত আলোচনা করব।
সামান্তরিক বা প্যারালেল লাইনস নিয়ে জেনে নেওয়া খুবই গুরুত্বপূর্ণ, কারণ এর ব্যবহার ঘটে জ্যামিতি, ট্রিগনোমেট্রি, ভৌতবিজ্ঞান এবং অন্যান্য বিষয়ে। তাই আমাদের জন্য এটি শেখা খুবই জরুরি। আসুন আজ আমরা সামান্তরিক সম্পর্কে গভীরভাবে জেনে নিই।
আশা করি এই পোস্ট আপনাদের কাজে লাগবে। এই বিষয়ে যে কোন প্রশ্ন থাকলে কমেন্ট করে জানাতে পারেন।
সামান্তরিক (Parallelogram) শব্দটি এসেছে গ্রীক ভাষার 'প্যারালেলোগ্রামন' থেকে। যার অর্থ "সমান্তরাল রেখার দ্বারা ঘিরে ধরা"। সামান্তরিক হলো একটি বিশেষ ধরনের চতুর্ভুজ যেখানে বিপরীত দুই বাহু একে অপরকে সমান্তরাল এবং সমান দৈর্ঘ্যের।
আরও পড়ুনঃ ত্রিভুজ কাকে বলে?
এছাড়াও, সামান্তরিকের বিপরীত কোণগুলো সমান হয় এবং বিপরীত দুই দীর্ঘক্ষেত্রের মধ্যবর্তী রেখাগুলো পরস্পর সমান্তরাল ও মাঝখানে প্রতিচ্ছেদ করে। সামান্তরিককে জ্যামিতিতে একটি গুরুত্বপূর্ণ চতুর্ভুজ হিসেবে বিবেচনা করা হয়।
সংক্ষেপে, যে চতুর্ভুজে বিপরীত বাহুগুলি সমান, সমান্তরাল এবং বিপরীত কোণগুলি সমান - সেটিকেই সামান্তরিক বলে।
তাহলে সামান্তরিক কাকে বলে এর উত্তরে বলা যায়, সামান্তরিক হলো এমন একটি চতুর্ভুজ যেখানে বিপরীত বাহুগুলো পরস্পর সমান্তরাল।
ধরুন একটি চতুর্ভুজ ABCD যেখানে,
বাহু AB এবং বাহু DC পরস্পর সমান্তরাল
বাহু AB এবং বাহু DC এর দৈর্ঘ্য সমান (উভয়েরই দৈর্ঘ্য 5 সেন্টিমিটার)
∠ABC = ∠BCD (কোণ ABC এবং কোণ BCD এর মাপ সমান, উভয়েরই 60 ডিগ্রি)
এখানে ABCD একটি সামান্তরিক চতুর্ভুজ কারণ এর বিপরীত দুটি বাহু (AB এবং DC) পরস্পর সমান্তরাল এবং সমদৈর্ঘ্যের। এছাড়াও বিপরীত কোণগুলো (∠ABC এবং ∠BCD) সমান।
সুতরাং, এটি সামান্তরিকের একটি প্রত্যক্ষ উদাহরণ।
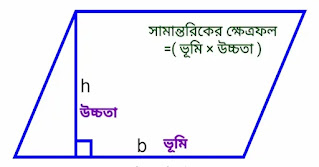
অর্থাৎ একটি সামান্তরিকের ক্ষেত্রফল হল একটি সামান্তরিকের চারটি বাহুর মধ্যে আবদ্ধ স্থান। এটি গণনা করা যেতে পারে যদি আমরা সামান্তরিকের ভূমি এবং উচ্চতা জানি।
মনে করি, একটি সামান্তরিকের ভূমি b এবং উচ্চতা h.
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক অর্থাৎ,
সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক।
উদাহরণ-১
একটি সামান্তরিকের ভূমি ১২ সেমি এবং উচ্চতা ১৮ সেমি হলে সামান্তরিকের ক্ষেত্রফল নির্ণয় কর।
উত্তর:
সামান্তরিকটির ভূমি b = ১১ সেমি এবং উচ্চতা h = ১৮ সেমি।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল =( b × h ) বর্গ একক।
অর্থাৎ, সামান্তরিকের ক্ষেত্রফল =( ১২ × ১৮ ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = ২১৬ বর্গ সেমি।
উদাহরণ- ২
একটি সমান্তরালগ্রামের ক্ষেত্রফল নির্ণয় কর যার ভূমি ৫ সেমি এবং উচ্চতা ৮ সেমি।
উত্তর:
সামান্তরিকটির ভূমি b = ৫ সেমি এবং উচ্চতা h = ৮ সেমি।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল =( b × h ) বর্গ একক।
অর্থাৎ, সামান্তরিকের ক্ষেত্রফল =( ৫ × ৮ ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = ৪০ বর্গ সেমি।
এছাড়াও, সামান্তরিকের বিপরীত কোণগুলো সমান হয় এবং বিপরীত দুই দীর্ঘক্ষেত্রের মধ্যবর্তী রেখাগুলো পরস্পর সমান্তরাল ও মাঝখানে প্রতিচ্ছেদ করে। সামান্তরিককে জ্যামিতিতে একটি গুরুত্বপূর্ণ চতুর্ভুজ হিসেবে বিবেচনা করা হয়।
সামান্তরিক কাকে বলে :-
যে চতুর্ভুজের বিপরীত দুই বাহু পরস্পর সমান্তরাল এবং সমপরিমাপের কিন্তু কোণগুলো সমকোণ নয় তাকে সামান্তরিক বলে।সংক্ষেপে, যে চতুর্ভুজে বিপরীত বাহুগুলি সমান, সমান্তরাল এবং বিপরীত কোণগুলি সমান - সেটিকেই সামান্তরিক বলে।
তাহলে সামান্তরিক কাকে বলে এর উত্তরে বলা যায়, সামান্তরিক হলো এমন একটি চতুর্ভুজ যেখানে বিপরীত বাহুগুলো পরস্পর সমান্তরাল।
সামান্তরিকের উদাহরণ :-
সামান্তরিকের একটি বিস্তারিত উদাহরণ দেওয়া হল:ধরুন একটি চতুর্ভুজ ABCD যেখানে,
বাহু AB এবং বাহু DC পরস্পর সমান্তরাল
বাহু AB এবং বাহু DC এর দৈর্ঘ্য সমান (উভয়েরই দৈর্ঘ্য 5 সেন্টিমিটার)
∠ABC = ∠BCD (কোণ ABC এবং কোণ BCD এর মাপ সমান, উভয়েরই 60 ডিগ্রি)
এখানে ABCD একটি সামান্তরিক চতুর্ভুজ কারণ এর বিপরীত দুটি বাহু (AB এবং DC) পরস্পর সমান্তরাল এবং সমদৈর্ঘ্যের। এছাড়াও বিপরীত কোণগুলো (∠ABC এবং ∠BCD) সমান।
সুতরাং, এটি সামান্তরিকের একটি প্রত্যক্ষ উদাহরণ।
সামান্তরিকের সূত্র :-
সামান্তরিকের মৌলিক সূত্র হিসেবে ক্ষেত্রফলের পাশাপাশি পরিধি রয়েছে । এখন আমরা সামান্তরিকের সূত্র নিয়ে আলোচনা করবো অর্থাৎ সামান্তরিকের ক্ষেত্রফল ও পরিধি নিয়ে আলোচনা করবো।আরও পড়ুনঃ সামান্তরিক কাকে বলে?
সামান্তরিকের ক্ষেত্রফল :-
সামান্তরিকের ভূমি ও উচ্চতার গুণফলকেই সামান্তরিকের ক্ষেত্রফল বলে।অর্থাৎ একটি সামান্তরিকের ক্ষেত্রফল হল একটি সামান্তরিকের চারটি বাহুর মধ্যে আবদ্ধ স্থান। এটি গণনা করা যেতে পারে যদি আমরা সামান্তরিকের ভূমি এবং উচ্চতা জানি।
মনে করি, একটি সামান্তরিকের ভূমি b এবং উচ্চতা h.
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক অর্থাৎ,
সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক।
উদাহরণ-১
একটি সামান্তরিকের ভূমি ১২ সেমি এবং উচ্চতা ১৮ সেমি হলে সামান্তরিকের ক্ষেত্রফল নির্ণয় কর।
উত্তর:
সামান্তরিকটির ভূমি b = ১১ সেমি এবং উচ্চতা h = ১৮ সেমি।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল =( b × h ) বর্গ একক।
অর্থাৎ, সামান্তরিকের ক্ষেত্রফল =( ১২ × ১৮ ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = ২১৬ বর্গ সেমি।
উদাহরণ- ২
একটি সমান্তরালগ্রামের ক্ষেত্রফল নির্ণয় কর যার ভূমি ৫ সেমি এবং উচ্চতা ৮ সেমি।
উত্তর:
সামান্তরিকটির ভূমি b = ৫ সেমি এবং উচ্চতা h = ৮ সেমি।
আমরা জানি,
সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক।
∴ সামান্তরিকের ক্ষেত্রফল =( b × h ) বর্গ একক।
অর্থাৎ, সামান্তরিকের ক্ষেত্রফল =( ৫ × ৮ ) বর্গ সেমি।
∴ সামান্তরিকের ক্ষেত্রফল = ৪০ বর্গ সেমি।
আরও পড়ুনঃ বৃত্ত কাকে বলে?
একইভাবে, একটি সামান্তরিকের পরিধি হল সমান্তরালগ্রামের সীমানার মোট দূরত্ব। পরিধির মান গণনা করার জন্য, আমাদের এর দৈর্ঘ্য এবং প্রস্থের মানগুলি জানতে হবে।
সামান্তরিকের চারটি বাহুর দৈর্ঘ্যের সমষ্টিকে সামান্তরিকের পরিধি বলা হয়।
অর্থাৎ, যদি সামান্তরিকের চারটি বাহুর দৈর্ঘ্য যদি a, b, c এবং d হয়, তাহলে সামান্তরিকের পরিধি = a + b + c + d
আর যে কোন দুটি বাহু দেওয়া থাকলেও সামান্তরিকের পরিধি বের করা যায়, যেহেতু বাকি দুটি বাহুও সমান দৈর্ঘ্যের।
মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক এবং b একক।
সুতরাং, সামান্তরিকের পরিধির সূত্রটি হবে-
সামান্তরিকের পরিধি = (a+b+a+b) একক।
বা, সামান্তরিকের পরিধি = (2a+2b) একক।
∴ সামান্তরিকের পরিধি = 2(a+b) একক।
∴ সামান্তরিকের পরিধি = ২ ⨯(সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক।
উদাহরণ -
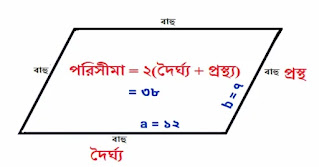
একটি সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য ১২ সেমি ও ৭ সেমি হলে সামান্তরিকের পরিধি নির্ণয় কর।
উত্তর:
মনেকরি, সামান্তরিকটির সন্নিহিত বাহু দুইটি a = ১২ সেমি এবং b = ৭ সেমি।
আমরা জানি,
সামান্তরিকের পরিধি = ২ ⨯(সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক।
∴ সামান্তরিকের পরিধি = 2(a+b) একক
বা, সামান্তরিকের পরিধি = ২(১২+৭) সেমি
বা, সামান্তরিকের পরিধি = (২ ⨯ ১৯) সেমি
∴ সামান্তরিকের পরিধি = ৩৮ সেমি।
1. সামান্তরিকের বিপরীত বাহু দ্বয় পরস্পর সমান - সামান্তরিকের যে বাহুগুলো একে অপরের বিপরীতে অবস্থিত, সেগুলোর দৈর্ঘ্য সমান থাকে।
2. সামান্তরিকের বিপরীত কোণগুলো পরস্পর সমান - যে কোণগুলো সামান্তরিকের বিপরীত শীর্ষে অবস্থিত, সেগুলোর মাপ সমান থাকে।
3. সামান্তরিকের যেকোন দুইটি সন্নিহিত কোণ পরস্পরের সম্পূরক - সামান্তরিকের যে কোণগুলো এক শীর্ষে সংযুক্ত, সেগুলোর যোগ 180 ডিগ্রি হয়।
4. সামান্তরিকের কর্ণদ্বয় অসমান - একই সামান্তরিকের দুই কর্ণের মাপ সমান থাকে না।
5. কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে - কর্ণ দুটি সামান্তরিককে দুই সমান অংশে ভাগ করে।
6. কর্ণ দিয়ে সর্বসম ত্রিভুজ তৈরি - প্রতিটি কর্ণ দিয়ে সামান্তরিককে দুইটি সর্বসম ত্রিভুজে ভাগ করা যায়।
7. কোণদ্বয়ের যোগ 180 ডিগ্রি - সামান্তরিকের যেকোন দুইটি সন্নিহিত কোণের যোগ 180 ডিগ্রি হয়।
8. বাহুর ও কর্ণের বর্গক্ষেত্র সমান - সামান্তরিকের বাহুতে ও কর্ণে অঙ্কিত বর্গক্ষেত্রের যোগফল সমান থাকে।
এভাবে সামান্তরিকের ব্যবহার রয়েছে বিভিন্ন ক্ষেত্রে। জ্যামিতি থেকে শুরু করে দৈনন্দিন জীবনের বিভিন্ন জায়গায় সামান্তরিকের প্রয়োজনীয়তা রয়েছে।
১) অসমান - সামান্তরিকের উভয় কর্ণের মাপ পরস্পর অসমান থাকে।
২) সমদ্বিখন্ডনশীল - কর্ণদ্বয় সামান্তরিককে দুই সমান অংশে ভাগ করে।
৩) সর্বসম ত্রিভুজ তৈরি - প্রতিটি কর্ণ দিয়ে সামান্তরিককে দুইটি সর্বসম ত্রিভুজে ভাগ করা যায়।
৪) কোণদ্বয়ের যোগ ১৮০ ডিগ্রি - সামান্তরিকের যেকোন দুইটি সন্নিহিত কোণের যোগ ১৮০ ডিগ্রি হয়।
৫) বর্গক্ষেত্র সমান - কর্ণ ও বাহুর বর্গক্ষেত্রের যোগফল সমান থাকে।
এসব বৈশিষ্ট্য রয়েছে সামান্তরিকের কর্ণদ্বয়ে।
২. বিপরীত কোণসমূহ পরস্পর সমান হয়।
৩. কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
সামান্তরিকের পরিধি :-
যেকোনো আকৃতির পরিধি হল আকৃতির চারপাশে আচ্ছাদিত মোট দূরত্ব বা যেকোনো আকৃতির মোট দৈর্ঘ্য।একইভাবে, একটি সামান্তরিকের পরিধি হল সমান্তরালগ্রামের সীমানার মোট দূরত্ব। পরিধির মান গণনা করার জন্য, আমাদের এর দৈর্ঘ্য এবং প্রস্থের মানগুলি জানতে হবে।
সামান্তরিকের চারটি বাহুর দৈর্ঘ্যের সমষ্টিকে সামান্তরিকের পরিধি বলা হয়।
অর্থাৎ, যদি সামান্তরিকের চারটি বাহুর দৈর্ঘ্য যদি a, b, c এবং d হয়, তাহলে সামান্তরিকের পরিধি = a + b + c + d
আর যে কোন দুটি বাহু দেওয়া থাকলেও সামান্তরিকের পরিধি বের করা যায়, যেহেতু বাকি দুটি বাহুও সমান দৈর্ঘ্যের।
মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটির দৈর্ঘ্য a একক এবং b একক।
সুতরাং, সামান্তরিকের পরিধির সূত্রটি হবে-
সামান্তরিকের পরিধি = (a+b+a+b) একক।
বা, সামান্তরিকের পরিধি = (2a+2b) একক।
∴ সামান্তরিকের পরিধি = 2(a+b) একক।
∴ সামান্তরিকের পরিধি = ২ ⨯(সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক।
উদাহরণ -
একটি সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য ১২ সেমি ও ৭ সেমি হলে সামান্তরিকের পরিধি নির্ণয় কর।
উত্তর:
মনেকরি, সামান্তরিকটির সন্নিহিত বাহু দুইটি a = ১২ সেমি এবং b = ৭ সেমি।
আমরা জানি,
সামান্তরিকের পরিধি = ২ ⨯(সন্নিহিত বাহুদ্বয়ের সমষ্টি) একক।
∴ সামান্তরিকের পরিধি = 2(a+b) একক
বা, সামান্তরিকের পরিধি = ২(১২+৭) সেমি
বা, সামান্তরিকের পরিধি = (২ ⨯ ১৯) সেমি
∴ সামান্তরিকের পরিধি = ৩৮ সেমি।
সামান্তরিকের বৈশিষ্ট্য :-
এখন আমরা সামান্তরিকের বৈশিষ্ট্যগুলো সম্পর্কে আলোচনা করবো। সামান্তরিকের ৩ ও চারটি বৈশিষ্ট্য প্রধান রয়েছে যা আলোচনা করবো, সেই সাথে কিভাবে সামান্তরিককে অন্য চতুর্ভুজ থেকে আলাদা করে, সামান্তরিকের ব্যবহার কোথায় কোথায় - এসব নিয়ে আলোচনা করা হবে।1. সামান্তরিকের বিপরীত বাহু দ্বয় পরস্পর সমান - সামান্তরিকের যে বাহুগুলো একে অপরের বিপরীতে অবস্থিত, সেগুলোর দৈর্ঘ্য সমান থাকে।
2. সামান্তরিকের বিপরীত কোণগুলো পরস্পর সমান - যে কোণগুলো সামান্তরিকের বিপরীত শীর্ষে অবস্থিত, সেগুলোর মাপ সমান থাকে।
3. সামান্তরিকের যেকোন দুইটি সন্নিহিত কোণ পরস্পরের সম্পূরক - সামান্তরিকের যে কোণগুলো এক শীর্ষে সংযুক্ত, সেগুলোর যোগ 180 ডিগ্রি হয়।
4. সামান্তরিকের কর্ণদ্বয় অসমান - একই সামান্তরিকের দুই কর্ণের মাপ সমান থাকে না।
5. কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে - কর্ণ দুটি সামান্তরিককে দুই সমান অংশে ভাগ করে।
6. কর্ণ দিয়ে সর্বসম ত্রিভুজ তৈরি - প্রতিটি কর্ণ দিয়ে সামান্তরিককে দুইটি সর্বসম ত্রিভুজে ভাগ করা যায়।
7. কোণদ্বয়ের যোগ 180 ডিগ্রি - সামান্তরিকের যেকোন দুইটি সন্নিহিত কোণের যোগ 180 ডিগ্রি হয়।
8. বাহুর ও কর্ণের বর্গক্ষেত্র সমান - সামান্তরিকের বাহুতে ও কর্ণে অঙ্কিত বর্গক্ষেত্রের যোগফল সমান থাকে।
সামান্তরিকের ব্যবহার :-
- - জ্যামিতি: সামান্তরিক জ্যামিতিতে ব্যবহৃত হয় বিভিন্ন সমীকরণ, প্রমেয় এবং গুণ প্রমাণ করার জন্য। এছাড়াও ক্ষেত্রফল, পরিসীমা ইত্যাদি নির্ণয়ে ব্যবহৃত হয়।
- - ভৌতবিজ্ঞান: ভৌতবিজ্ঞানে বিভিন্ন ক্ষেত্রে যেমন ক্ষেত্রবিদ্যুৎ, গতিবিদ্যা ইত্যাদিতে সামান্তরিকের ব্যবহার হয়।
- - প্রকৌশলবিদ্যা: সামান্তরিকের ধরন বিবেচনা করে নকশা তৈরি, প্রকৌশলগত সমস্যা সমাধান করা হয়।
- - দৈনন্দিন জীবন: সামান্তরিকের ধারণা ব্যবহার করে বিভিন্ন জিনিসের আয়তন, ক্ষেত্রফল ইত্যাদি হিসাব করা যায়।
এভাবে সামান্তরিকের ব্যবহার রয়েছে বিভিন্ন ক্ষেত্রে। জ্যামিতি থেকে শুরু করে দৈনন্দিন জীবনের বিভিন্ন জায়গায় সামান্তরিকের প্রয়োজনীয়তা রয়েছে।
সামান্তরিকের কর্ণের বৈশিষ্ট্য :-
সামান্তরিকের কর্ণদ্বয়ের নিম্নোক্ত বৈশিষ্ট্যগুলো রয়েছে:১) অসমান - সামান্তরিকের উভয় কর্ণের মাপ পরস্পর অসমান থাকে।
২) সমদ্বিখন্ডনশীল - কর্ণদ্বয় সামান্তরিককে দুই সমান অংশে ভাগ করে।
৩) সর্বসম ত্রিভুজ তৈরি - প্রতিটি কর্ণ দিয়ে সামান্তরিককে দুইটি সর্বসম ত্রিভুজে ভাগ করা যায়।
৪) কোণদ্বয়ের যোগ ১৮০ ডিগ্রি - সামান্তরিকের যেকোন দুইটি সন্নিহিত কোণের যোগ ১৮০ ডিগ্রি হয়।
৫) বর্গক্ষেত্র সমান - কর্ণ ও বাহুর বর্গক্ষেত্রের যোগফল সমান থাকে।
এসব বৈশিষ্ট্য রয়েছে সামান্তরিকের কর্ণদ্বয়ে।
- সামান্তরিকের কর্ণদ্বয় কেমন?
- বর্গক্ষেত্র কি একটি সমান্তরাল বৃত্ত?
- আয়তক্ষেত্র কি একটি সমান্তরালগ্রাম?
- সামান্তরিকের ৩টি বৈশিষ্ট্য?
২. বিপরীত কোণসমূহ পরস্পর সমান হয়।
৩. কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।









0 মন্তব্যসমূহ
Please do not enter any spam link in the comment box.