বৃত্ত কাকে বলে তা সহজ ভাষায় বললে, একটি স্থির বিন্দু হতে যেসব বিন্দুর দূরত্ব সমান তাদের সেটকে একটি বৃত্ত বলে।
স্থির বিন্দুকে বৃত্তটির কেন্দ্র এবং স্থির দূরত্বকে ইহার ব্যাসার্ধ বলা হয়।
গ্রিক শব্দ Kirkos থেকে বৃত্ত (Circle) শব্দটি নেওয়া হয়েছে যার অর্থ আংটা। গাড়ীর ঢাকা, চন্দ্র, সূর্য গাছের কান্ডের প্রছচ্ছেদ প্রভৃতি বস্তু বৃত্তাকার দেখায়। জ্যামিতি, জ্যোতির্বিদ্যা, ক্যালকুলাস, কম্পিউটার গ্রাফিক্স ডিজাইন ইত্যাদিতে বৃত্ত ব্যবহার হয়ে থাকে।
এই পোস্টে আমরা বৃত্ত কাকে বলে? তা জানার সাথে সাথে বৃত্ত সম্পর্কিত বিভিন্ন ধারণা যেমন কেন্দ্র, ব্যাস, ব্যাসার্ধ, জ্যা ইত্যাদি বিষয়ে জ্ঞান অর্জন করবো। এছাড়াও সমতলে কোনো বৃত্তের জ্যা, চাপ, বৃত্তে অন্তর্লিখিত চতুর্ভূজ, বৃত্তের ছেদক ও স্পর্শক সম্পর্কিত প্রতিজ্ঞার আলোচনা করা হবে।
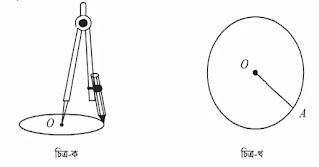
কম্পাসের কাঁটাটি কাগজের উপর চেপে ধরে অপর প্রান্তে সংযুক্ত পেন্সিলটি কাগজের উপর চারদিকে ঘুরিয়ে আনলেই একটি বৃত্ত আকা হয়ে থাকে, যা নীচের চিত্র (ক)-তে দেখানো হয়েছে।
তাহলে দেখা যাচ্ছে বৃত্ত আঁকার সময় নির্দিষ্ট একটি বিন্দু থেকে সমদূরবর্তী বিন্দুগুলোকে আঁকা হয়। এই নির্দিষ্ট বিন্দুটি বৃত্তের কেন্দ্র। কেন্দ্র থেকে সমদূরবর্তী যেকোনো বিন্দুর দূরত্ব হলো বৃত্তের ব্যাসার্ধ।
চিত্র (খ)-তে O হলো বৃত্তের কেন্দ্র এবং OA হলো বৃত্তের ব্যাসার্ধ।
বৃত্ত, বৃত্তের অভ্যন্তর ও বৃত্তের বহির্ভাগ সমতলের তিনটি উপসেট যারা পরস্পর নিশ্ছেদ। বৃত্তের বহির্ভাগের কোনো বিন্দুকে বৃত্তের একটি বহিঃস্থ বিন্দু বলা হয়।
বৃত্তের অভ্যন্তরস্থ দুইটি বিন্দুর সংযোজক রেখাংশ সম্পূর্ণভাবে বৃত্তের অভ্যন্তরেই থাকে।
চিত্রে, P বৃত্তের অভ্যন্তরস্থ একটি বিন্দু এবং Q বৃত্তের বহিঃস্থ একটি বিন্দু। PQ রেখাংশ বৃত্তটিকে কেবল R বিন্দুতে ছেদ করে।
(খ) যদি কোনো বৃত্তের একটি বিন্দু অপর একটি বৃত্তের অভ্যন্তরে থাকে এবং প্রথমোক্ত বৃত্তের অপর একটি বিন্দু শেষোক্ত বৃত্তের বহির্ভাগে থাকে, তবে বৃত্তদ্বয়ের দুইটি ও কেবল দুইটি ছেদ বিন্দু থাকে।
ব্যাস = 2 × ব্যাসার্ধ।
আরও পড়ুনঃ বিন্দু কাকে বলে?
বৃত্তের পরিধি = 2πr একক।
কোনো বৃত্তের জ্যা যদি বৃত্তটির কেন্দ্র দিয়ে যায় তবে জ্যাটিকে বৃত্তের ব্যাস বলা হয়, অর্থাৎ বৃত্তের কেন্দ্রগামী যেকোনো জ্যা হলো ব্যাস।
নীচের চিত্রে, বৃত্তটির কেন্দ্র O এবং AB ও AC বৃত্তটির দুইটি জ্যা। AB জ্যা টি ব্যাস, কারণ জ্যা টি বৃত্তটির কেন্দ্রগামী। OA ও OB বৃত্তের দুইটি ব্যাসার্ধ এবং O বিন্দুটি AB জ্যা-এর মধ্যবিন্দু। সুতরাং, বৃত্তের কেন্দ্র প্রত্যেক ব্যাসের মধ্যবিন্দু।
কোনো বৃত্তে A ও B দুইটি নির্দিষ্ট বিন্দু হলে A, B এবং AB একপাশে অবস্থিত বৃত্তের বিশ্বসমূহের সেটকে বৃত্তটির একটি চাপ বলা হয়।
A ও B এই চাপের প্রান্তবিন্দু এবং চাপের অন্য সকল বিন্দু তার অন্তঃস্থ বিন্দু। একটি চাপের অন্তঃস্থ বিন্দু C হলে চাপটিকে ACB চাপ বলা হয় এবং ACB প্রতীক দ্বারা প্রকাশ করা হয়। তবে কখনও কখনও তাদেরকে AB চাপও বলা হয়। নিচের প্রত্যেকটি চিত্রে ^ACB একটি চাপ।
উপচাপ: 'ক' চিত্রে ACB চাপের অন্তঃস্থ বিন্দুসমূহ AB -এর যে পাশে কেন্দ্র আছে তার বিপরীত পাশে অবস্থিত। এক্ষেত্রে ACB চাপকে উপচাপ বলা হয়।
অধিচাপ: 'খ' চিত্রে ACB চাপের সকল বিন্দু এবং কেন্দ্র AB -এর একই পাশে অবস্থিত। এক্ষেত্রে ACB চাপকে অধিচাপ বলা হয়।
অর্ধবৃত্ত: 'গ' চিত্রে AB রেখাংশ কেন্দ্র দিয়ে যায়। তাই ACB চাপকে অর্ধবৃত্ত বলা হয়।
অনুবন্ধী: 'ঘ' চিত্রে ACB চাপ ও ADB চাপ উভয়েরই প্রান্ত বিন্দু AB এবং C ও D বিন্দু AB-এর উভয় পার্শ্বে অবস্থিত। তাই ACB ও ADB চাপ দুইটি একটি অপরটির অনুবন্ধী এবং একটি উপচাপ হলে অপরটি হবে অধিচাপ।
সূত্র (ক)। প্রত্যেক বৃত্তের নির্দিষ্ট দৈর্ঘ্য রয়েছে এবং এই দৈর্ঘ্য বৃত্তের ব্যাসের দৈর্ঘ্যের আনুপাতিক।
সূত্র (খ)। যে বৃত্তের ব্যাসের দৈর্ঘ্য এক একক সেই বৃত্তের দৈর্ঘ্য = একক, যেখানে π = 3.1415926535897932……. একটি অমূলদ সংখ্যা। বিভিন্ন হিসাবে নির্দিষ্ট দশমিক ঘর পর্যন্ত π এর আসন্ন মান ব্যবহার করা হয়।
বৃত্তের দৈর্ঘ্যকে তার পরিধি বলা হয়।
সূত্র (গ)। কোনো বৃত্তের ব্যাসার্ধ r হলে, তার পরিধি c = 2πr.
প্রমাণ : বৃত্তের ব্যাসের দৈর্ঘ্য d = 2r
সূত্র (ক) থেকে বলা যায় c = kd যেখানে k একটি ধ্রুবক।
কিন্তু সূত্র (খ) থেকে দেখা যায় যে, π = k।
সুতরাং c = rd = π (2r) = 2πr .
ধরুন, P কেন্দ্রিক ও Q কেন্দ্রিক বৃত্ত দুইটির প্রত্যেকের ব্যাসার্ধ r । তারা সমান বৃত্ত। উভয় বৃত্তের দৈর্ঘ্য c = 2πr. সকল সমান বৃত্তের দৈর্ঘ্য সমান।
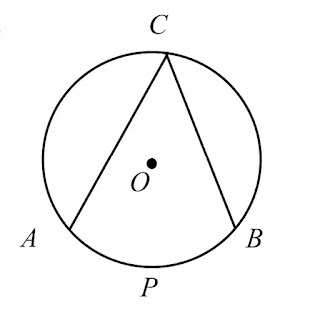
চিত্রে <ACB একটি বৃত্তস্থ কোণ। প্রত্যেক বৃত্তস্থ কোণ বৃত্তে একটি চাপ খণ্ডিত করে। এই চাপ উপচাপ, অর্ধবৃত্ত অথবা অধিচাপ হতে পারে।
একটি বৃত্তস্থ কোণ বৃত্তে যে চাপ খণ্ডিত করে, কোণটি সেই চাপের ওপর দণ্ডায়মান এবং খণ্ডিত চাপের অনুবন্ধী চাপে অস্তলিখিত বলা হয়।
চিত্রে <ACB বৃত্তস্থ কোণটি APB চাপকে খণ্ডিত করে। অতএব, <ACB, APB চাপের ওপর দণ্ডায়মান এবং ACB চাপে অন্তর্লিখিত একটি বৃত্তস্থ কোণ। এখানে APB ও ACBএকে অপরের অনুবন্ধী চাপ।
চিত্রে ABCD চতুর্ভুজটি বৃত্তে অন্তর্লিখিত হয়েছে। বৃত্তটি চতুর্ভুজ ABCD-এর পরিবৃত্ত। এক্ষেত্রে ABCD-এর শীর্ষবিন্দুগুলো সমবৃত্ত হয়েছে বলা হয় অর্থাৎ A, B, C, D সমবৃত্ত।
মন্তব্য: সমরেখ নয় এমন তিনটি বিন্দু দিয়ে সবসময় একটি বৃত্ত অঙ্কন করা যায়। সুতরাং প্রত্যেক ত্রিভুজকে বৃত্তে অন্তর্লিখিত করা যায়। কিন্তু ত্রিভুজ ব্যতীত অন্য কোনো বহুভুজকে সবসময় বৃত্তে অন্তর্লিখিত করা যায় না।
(১) চিত্র-ক এ বৃত্ত ও সরলরেখার কোনো সাধারণ বিন্দু নেই,
(২) চিত্র-খ এ সরলরেখাটি বৃত্তকে একটি বিন্দুতে স্পর্শ করেছে,
(৩) চিত্র-গ এ সরলরেখাটি বৃত্তকে দুইটি বিন্দুতে ছেদ করেছে, অর্থাৎ সমতলস্থ একটি বৃত্ত ও একটি সরলরেখার সর্বাধিক দুইটি সাধারণ বিন্দু বা ছেদবিন্দু থাকতে পারে।
অতএব উপরের চিত্র অনুসারে আমরা বৃত্তের ছেদক ও স্পর্শকের সংজ্ঞা নিম্নলিখিতভাবে দিতে পারি।
সমতলস্থ একটি বৃত্ত ও একটি সরলরেখার যদি দুইটি ছেদবিন্দু থাকে তবে রেখাটিকে বৃত্তটির একটি ছেদক বলা হয়।
কিন্তু যদি একটি ও কেবল একটি সাধারণ বিন্দু থাকে তবে রেখাটিকে বৃত্তটির একটি স্পর্শক বলা হয়।
শেষোক্ত ক্ষেত্রে, সাধারণ বিন্দুটিকে ঐ স্পর্শকের স্পর্শবিন্দু বলা হয়।
উপরের চিত্রে একটি বৃত্ত ও একটি সরলরেখার পারস্পরিক অবস্থান দেখানো হয়েছে। চিত্র- গ এ PQ সরলরেখাটি বৃত্তকে A ও B দুইটি বিন্দুতে ছেদ করেছে এবং চিত্র- খ এ PQ সরলরেখাটি বৃত্তকে A বিন্দুতে স্পর্শ করেছে, অর্থাৎ PQ বৃত্তটির স্পর্শক ও A এই স্পর্শকের স্পর্শবিন্দু।
মন্তব্য। বৃত্তের প্রত্যেক জেদকের ছেদবিন্দুদ্বয়ের অন্তর্বর্তী সকল বিন্দু বৃত্তটির অভ্যন্তরে থাকে।
চিত্রে P বৃত্তস্থ বিন্দু, PT রশ্মি P বিন্দুতে বৃত্তের স্পর্শক এবং PQ রশ্মি বৃত্তটিকে Q বিন্দুতে ছেদ করেছে। PBQ চাপ <TPQ এর একান্তর বৃত্তাংশ।
স্থির বিন্দুকে বৃত্তটির কেন্দ্র এবং স্থির দূরত্বকে ইহার ব্যাসার্ধ বলা হয়।
গ্রিক শব্দ Kirkos থেকে বৃত্ত (Circle) শব্দটি নেওয়া হয়েছে যার অর্থ আংটা। গাড়ীর ঢাকা, চন্দ্র, সূর্য গাছের কান্ডের প্রছচ্ছেদ প্রভৃতি বস্তু বৃত্তাকার দেখায়। জ্যামিতি, জ্যোতির্বিদ্যা, ক্যালকুলাস, কম্পিউটার গ্রাফিক্স ডিজাইন ইত্যাদিতে বৃত্ত ব্যবহার হয়ে থাকে।
এই পোস্টে আমরা বৃত্ত কাকে বলে? তা জানার সাথে সাথে বৃত্ত সম্পর্কিত বিভিন্ন ধারণা যেমন কেন্দ্র, ব্যাস, ব্যাসার্ধ, জ্যা ইত্যাদি বিষয়ে জ্ঞান অর্জন করবো। এছাড়াও সমতলে কোনো বৃত্তের জ্যা, চাপ, বৃত্তে অন্তর্লিখিত চতুর্ভূজ, বৃত্তের ছেদক ও স্পর্শক সম্পর্কিত প্রতিজ্ঞার আলোচনা করা হবে।
বৃত্ত কাকে বলে :-
কোন সমতলে অবস্থিত একটি নির্দিষ্ট স্থির বিন্দু হতে চাপ, সর্বদা সমান দূরে থেকে অপর একটি চলন্ত বিন্দু এক বার ঘুরে এলে যে আবদ্ধ বক্র রেখা উৎপন্ন হয় তাকে বৃত্ত বলে।বৃত্তের সংজ্ঞা :-
যদি O সমতলের কোনো নির্দিষ্ট বিন্দু হয় এবং একটি নির্দিষ্ট ধনাত্মক বাস্তব সংখ্যা হয়, তবে সমতলস্থ যে সকল বিন্দু O থেকে A দূরত্বে অবস্থিত, তাদের সেটকে বৃত্ত বলা হয়।বৃত্ত আঁকার নিয়ম:-
বৃত্ত একটি সমতলীয় জ্যামিতিক চিত্র। নিখুঁতভাবে বৃত্ত আঁকার জন্য পেন্সিল কম্পাস ব্যবহার করা হয়।কম্পাসের কাঁটাটি কাগজের উপর চেপে ধরে অপর প্রান্তে সংযুক্ত পেন্সিলটি কাগজের উপর চারদিকে ঘুরিয়ে আনলেই একটি বৃত্ত আকা হয়ে থাকে, যা নীচের চিত্র (ক)-তে দেখানো হয়েছে।
তাহলে দেখা যাচ্ছে বৃত্ত আঁকার সময় নির্দিষ্ট একটি বিন্দু থেকে সমদূরবর্তী বিন্দুগুলোকে আঁকা হয়। এই নির্দিষ্ট বিন্দুটি বৃত্তের কেন্দ্র। কেন্দ্র থেকে সমদূরবর্তী যেকোনো বিন্দুর দূরত্ব হলো বৃত্তের ব্যাসার্ধ।
চিত্র (খ)-তে O হলো বৃত্তের কেন্দ্র এবং OA হলো বৃত্তের ব্যাসার্ধ।
বৃত্তের অভ্যন্তর ও বহির্ভাগ কাকে বলে:-
যদি কোনো বৃত্তের কেন্দ্র O এবং ব্যাসার্ধ A হয় তবে O থেকে সমতলের যে সকল বিন্দুর দূরত্ব থেকে কম তাদের সেটকে বৃত্তটির অভ্যন্তর এবং O থেকে সমতলের যে সকল বিন্দুর দূরত্ব A থেকে বেশি তাদের সেটকে বৃত্তটির বহির্ভাগ বলা হয়।বৃত্ত, বৃত্তের অভ্যন্তর ও বৃত্তের বহির্ভাগ সমতলের তিনটি উপসেট যারা পরস্পর নিশ্ছেদ। বৃত্তের বহির্ভাগের কোনো বিন্দুকে বৃত্তের একটি বহিঃস্থ বিন্দু বলা হয়।
বৃত্তের অভ্যন্তরস্থ দুইটি বিন্দুর সংযোজক রেখাংশ সম্পূর্ণভাবে বৃত্তের অভ্যন্তরেই থাকে।
বৃত্তের অবিচ্ছিন্নতা বিষয়ক দুইটি সূত্র:
(ক) কোনো বৃত্তের অভ্যন্তরস্থ একটি বিন্দু ও বহিঃস্থ একটি বিন্দুর সংযোজক রেখাংশ বৃত্তটিকে একটি ও কেবল একটি বিন্দুতে ছেদ করে।চিত্রে, P বৃত্তের অভ্যন্তরস্থ একটি বিন্দু এবং Q বৃত্তের বহিঃস্থ একটি বিন্দু। PQ রেখাংশ বৃত্তটিকে কেবল R বিন্দুতে ছেদ করে।
(খ) যদি কোনো বৃত্তের একটি বিন্দু অপর একটি বৃত্তের অভ্যন্তরে থাকে এবং প্রথমোক্ত বৃত্তের অপর একটি বিন্দু শেষোক্ত বৃত্তের বহির্ভাগে থাকে, তবে বৃত্তদ্বয়ের দুইটি ও কেবল দুইটি ছেদ বিন্দু থাকে।
বৃত্তের কেন্দ্র কাকে বলে :-
একটি বৃত্তের কেন্দ্র হল একটি বৃত্তের কেন্দ্রবিন্দু যেখান থেকে বৃত্তের বিন্দুগুলির সমস্ত দূরত্ব সমান। এই দূরত্বকে বৃত্তের ব্যাসার্ধ বলে।বৃত্তের অংশ :-
১. বৃত্তের ব্যাসার্ধ:
ব্যাসার্ধ হল বৃত্তের কেন্দ্রে একটি প্রান্তবিন্দু এবং বৃত্তের অপর প্রান্তবিন্দু সহ একটি রেখার অংশ।২. বৃত্তের ব্যাস:
একটি বৃত্তের কেন্দ্রের মধ্য দিয়ে যাওয়া একটি রেখার অংশ এবং বৃত্তের উপর এর শেষ বিন্দু রয়েছে, তাকে বৃত্তের ব্যাস বলে।ব্যাস = 2 × ব্যাসার্ধ।
৩. বৃত্তের ক্ষেত্রফল:
বৃত্তের ক্ষেত্রফল = πr² বর্গ এককআরও পড়ুনঃ বিন্দু কাকে বলে?
৪. বৃত্তের পরিধি:
একটি বৃত্তের পরিধি হল একটি বৃত্তের চারপাশের দূরত্ব। এটি অন্যান্য আকারের পরিধির সমান ।বৃত্তের পরিধি = 2πr একক।
৫. বৃত্তের জ্যা ও ব্যাস কাকে বলে :-
কোনো বৃত্তের দুইটি ভিন্ন বিন্দুর সংযোজক রেখাংশকে বৃত্তটির একটি জ্যা বলা হয়।কোনো বৃত্তের জ্যা যদি বৃত্তটির কেন্দ্র দিয়ে যায় তবে জ্যাটিকে বৃত্তের ব্যাস বলা হয়, অর্থাৎ বৃত্তের কেন্দ্রগামী যেকোনো জ্যা হলো ব্যাস।
নীচের চিত্রে, বৃত্তটির কেন্দ্র O এবং AB ও AC বৃত্তটির দুইটি জ্যা। AB জ্যা টি ব্যাস, কারণ জ্যা টি বৃত্তটির কেন্দ্রগামী। OA ও OB বৃত্তের দুইটি ব্যাসার্ধ এবং O বিন্দুটি AB জ্যা-এর মধ্যবিন্দু। সুতরাং, বৃত্তের কেন্দ্র প্রত্যেক ব্যাসের মধ্যবিন্দু।
৬. বৃত্তচাপ কাকে বলে :-
কোনো বৃত্তের দুইটি নির্দিষ্ট বিন্দু এবং ঐ বিন্দুদ্ধয়ের একপাশে অবস্থিত বৃত্তের বিন্দুসমূহের সেটকে বৃত্তটির একটি চাপ বলে।কোনো বৃত্তে A ও B দুইটি নির্দিষ্ট বিন্দু হলে A, B এবং AB একপাশে অবস্থিত বৃত্তের বিশ্বসমূহের সেটকে বৃত্তটির একটি চাপ বলা হয়।
A ও B এই চাপের প্রান্তবিন্দু এবং চাপের অন্য সকল বিন্দু তার অন্তঃস্থ বিন্দু। একটি চাপের অন্তঃস্থ বিন্দু C হলে চাপটিকে ACB চাপ বলা হয় এবং ACB প্রতীক দ্বারা প্রকাশ করা হয়। তবে কখনও কখনও তাদেরকে AB চাপও বলা হয়। নিচের প্রত্যেকটি চিত্রে ^ACB একটি চাপ।
উপচাপ: 'ক' চিত্রে ACB চাপের অন্তঃস্থ বিন্দুসমূহ AB -এর যে পাশে কেন্দ্র আছে তার বিপরীত পাশে অবস্থিত। এক্ষেত্রে ACB চাপকে উপচাপ বলা হয়।
অধিচাপ: 'খ' চিত্রে ACB চাপের সকল বিন্দু এবং কেন্দ্র AB -এর একই পাশে অবস্থিত। এক্ষেত্রে ACB চাপকে অধিচাপ বলা হয়।
অর্ধবৃত্ত: 'গ' চিত্রে AB রেখাংশ কেন্দ্র দিয়ে যায়। তাই ACB চাপকে অর্ধবৃত্ত বলা হয়।
অনুবন্ধী: 'ঘ' চিত্রে ACB চাপ ও ADB চাপ উভয়েরই প্রান্ত বিন্দু AB এবং C ও D বিন্দু AB-এর উভয় পার্শ্বে অবস্থিত। তাই ACB ও ADB চাপ দুইটি একটি অপরটির অনুবন্ধী এবং একটি উপচাপ হলে অপরটি হবে অধিচাপ।
বৃত্তের ও বৃত্তচাপের দৈর্ঘ্য :-
এ পর্যায়ে আমরা স্বীকার করে নিই যে-সূত্র (ক)। প্রত্যেক বৃত্তের নির্দিষ্ট দৈর্ঘ্য রয়েছে এবং এই দৈর্ঘ্য বৃত্তের ব্যাসের দৈর্ঘ্যের আনুপাতিক।
সূত্র (খ)। যে বৃত্তের ব্যাসের দৈর্ঘ্য এক একক সেই বৃত্তের দৈর্ঘ্য = একক, যেখানে π = 3.1415926535897932……. একটি অমূলদ সংখ্যা। বিভিন্ন হিসাবে নির্দিষ্ট দশমিক ঘর পর্যন্ত π এর আসন্ন মান ব্যবহার করা হয়।
বৃত্তের দৈর্ঘ্যকে তার পরিধি বলা হয়।
সূত্র (গ)। কোনো বৃত্তের ব্যাসার্ধ r হলে, তার পরিধি c = 2πr.
প্রমাণ : বৃত্তের ব্যাসের দৈর্ঘ্য d = 2r
সূত্র (ক) থেকে বলা যায় c = kd যেখানে k একটি ধ্রুবক।
কিন্তু সূত্র (খ) থেকে দেখা যায় যে, π = k।
সুতরাং c = rd = π (2r) = 2πr .
সমান বৃত্ত:-
যে সকল বৃত্তের ব্যাসার্ধ সমান, তাদের সমান বৃত্ত বলা হয়।ধরুন, P কেন্দ্রিক ও Q কেন্দ্রিক বৃত্ত দুইটির প্রত্যেকের ব্যাসার্ধ r । তারা সমান বৃত্ত। উভয় বৃত্তের দৈর্ঘ্য c = 2πr. সকল সমান বৃত্তের দৈর্ঘ্য সমান।
বৃত্তস্থ কোণ :-
একটি কোণের শীর্ষবিন্দু কোনো বৃত্তের একটি বিন্দু হলে এবং কোণটির প্রত্যেক বাহুতে শীর্ষবিন্দু ছাড়াও বৃত্তের একটি বিন্দু থাকলে কোণটিকে বৃত্তস্থ কোণ বা বৃত্তে অন্তর্লিখিত কোণ বলা হয়।চিত্রে <ACB একটি বৃত্তস্থ কোণ। প্রত্যেক বৃত্তস্থ কোণ বৃত্তে একটি চাপ খণ্ডিত করে। এই চাপ উপচাপ, অর্ধবৃত্ত অথবা অধিচাপ হতে পারে।
একটি বৃত্তস্থ কোণ বৃত্তে যে চাপ খণ্ডিত করে, কোণটি সেই চাপের ওপর দণ্ডায়মান এবং খণ্ডিত চাপের অনুবন্ধী চাপে অস্তলিখিত বলা হয়।
চিত্রে <ACB বৃত্তস্থ কোণটি APB চাপকে খণ্ডিত করে। অতএব, <ACB, APB চাপের ওপর দণ্ডায়মান এবং ACB চাপে অন্তর্লিখিত একটি বৃত্তস্থ কোণ। এখানে APB ও ACBএকে অপরের অনুবন্ধী চাপ।
বৃত্তে অন্তর্লিখিত চতুর্ভুজ:
যদি কোনো চতুর্ভুজের চারটি শীর্ষবিন্দু একই বৃত্তের উপর অবস্থিত হয়, তাহলে চতুর্ভুজটি ঐ বৃত্তে অন্তর্লিখিত হয়েছে বলা হয়। সেক্ষেত্রে বৃত্তটিকে চতুর্ভুজটির পরিবৃত্ত বলা হয়।চিত্রে ABCD চতুর্ভুজটি বৃত্তে অন্তর্লিখিত হয়েছে। বৃত্তটি চতুর্ভুজ ABCD-এর পরিবৃত্ত। এক্ষেত্রে ABCD-এর শীর্ষবিন্দুগুলো সমবৃত্ত হয়েছে বলা হয় অর্থাৎ A, B, C, D সমবৃত্ত।
মন্তব্য: সমরেখ নয় এমন তিনটি বিন্দু দিয়ে সবসময় একটি বৃত্ত অঙ্কন করা যায়। সুতরাং প্রত্যেক ত্রিভুজকে বৃত্তে অন্তর্লিখিত করা যায়। কিন্তু ত্রিভুজ ব্যতীত অন্য কোনো বহুভুজকে সবসময় বৃত্তে অন্তর্লিখিত করা যায় না।
বৃত্তের ছেদক ও স্পর্শক :-
নিচের চিত্রগুলো লক্ষ্য করুন। সমতলে একটি বৃত্ত ও একটি সরলরেখার পারস্পরিক তিনটি অবস্থান থাকার সম্ভাবনা রয়েছে। যেমন(১) চিত্র-ক এ বৃত্ত ও সরলরেখার কোনো সাধারণ বিন্দু নেই,
(২) চিত্র-খ এ সরলরেখাটি বৃত্তকে একটি বিন্দুতে স্পর্শ করেছে,
(৩) চিত্র-গ এ সরলরেখাটি বৃত্তকে দুইটি বিন্দুতে ছেদ করেছে, অর্থাৎ সমতলস্থ একটি বৃত্ত ও একটি সরলরেখার সর্বাধিক দুইটি সাধারণ বিন্দু বা ছেদবিন্দু থাকতে পারে।
অতএব উপরের চিত্র অনুসারে আমরা বৃত্তের ছেদক ও স্পর্শকের সংজ্ঞা নিম্নলিখিতভাবে দিতে পারি।
সমতলস্থ একটি বৃত্ত ও একটি সরলরেখার যদি দুইটি ছেদবিন্দু থাকে তবে রেখাটিকে বৃত্তটির একটি ছেদক বলা হয়।
কিন্তু যদি একটি ও কেবল একটি সাধারণ বিন্দু থাকে তবে রেখাটিকে বৃত্তটির একটি স্পর্শক বলা হয়।
শেষোক্ত ক্ষেত্রে, সাধারণ বিন্দুটিকে ঐ স্পর্শকের স্পর্শবিন্দু বলা হয়।
উপরের চিত্রে একটি বৃত্ত ও একটি সরলরেখার পারস্পরিক অবস্থান দেখানো হয়েছে। চিত্র- গ এ PQ সরলরেখাটি বৃত্তকে A ও B দুইটি বিন্দুতে ছেদ করেছে এবং চিত্র- খ এ PQ সরলরেখাটি বৃত্তকে A বিন্দুতে স্পর্শ করেছে, অর্থাৎ PQ বৃত্তটির স্পর্শক ও A এই স্পর্শকের স্পর্শবিন্দু।
মন্তব্য। বৃত্তের প্রত্যেক জেদকের ছেদবিন্দুদ্বয়ের অন্তর্বর্তী সকল বিন্দু বৃত্তটির অভ্যন্তরে থাকে।
একান্তর বৃত্তাংশ :-
একটি কোণ যদি এমন হয় যে তার শীর্ষবিন্দু কোনো বৃত্তের একটি বিন্দু এবং একটি বাহু বৃত্তটির একটি স্পর্শক ও অপরটি বৃত্তটির একটি ছেদক, তবে কোণটি বৃত্তটির যে চাপ ছিন্ন করে সেই চাপের অনুবন্ধী চাপকে কোণটির একান্তর বৃত্তাংশ বা একান্তর চাপ বলা হয়।চিত্রে P বৃত্তস্থ বিন্দু, PT রশ্মি P বিন্দুতে বৃত্তের স্পর্শক এবং PQ রশ্মি বৃত্তটিকে Q বিন্দুতে ছেদ করেছে। PBQ চাপ <TPQ এর একান্তর বৃত্তাংশ।
বৃত্তাংশ কাকে বলে :-
বৃত্তের একটি জ্যা ও একটি চাপ দ্বারা গঠিত অঞ্চলকে বৃত্তাংশ বলে।বৃত্ত কলা কাকে বলে :-
বৃত্তের দুইটি ব্যাসার্ধ ও একটি চাপ দ্বারা গঠিত অঞ্চলকে বৃত্তকলা বা বৃত্তীয় ক্ষেত্র বলে।বৃত্তের বৈশিষ্ট্য :-
বৃত্তের গুরুত্বপূর্ণ মৌলিক বৈশিষ্ট্যগুলি নিম্নরূপ:- একটি বৃত্তের বাইরেররেখাটি কেন্দ্র থেকে সমান দূরত্বে অবস্থিত।
- বৃত্তের ব্যাস এটিকে দুটি সমান অংশে বিভক্ত করে।
- যে সকল বৃত্তের ব্যাসার্ধ সমান তারা একে অপরের সাথে সঙ্গতিপূর্ণ।
- যে বৃত্তগুলি আকারে ভিন্ন বা ভিন্ন ব্যাসার্ধ রয়েছে সেগুলি একই রকম।
- বৃত্তের ব্যাস হল বৃহত্তম জ্যা এবং ব্যাসার্ধের দ্বিগুণ।ভক্ত করে।
- যে সকল বৃত্তের ব্যাসার্ধ সমান তারা একে অপরের সাথে সঙ্গতিপূর্ণ।
- যে বৃত্তগুলি আকারে ভিন্ন বা ভিন্ন ব্যাসার্ধ রয়েছে সেগুলি একই রকম।
- বৃত্তের ব্যাস হল বৃহত্তম জ্যা এবং ব্যাসার্ধের দ্বিগুণ।















0 মন্তব্যসমূহ
Please do not enter any spam link in the comment box.